『 DeepPose: Human Pose Estimation via Deep Neural Networks. CVPR. 2014. 』
지금까지 여러 Pose Estimation 논문을 읽어보았지만, 아직 Pose Estimation의 초창기 발전 과정부터 논문을 읽어오지 않았었다. 따라서 관련 논문도 준비할 겸 이번 기회에 Pose Estimation과 딥러닝이 만나기 시작한 시점부터 논문을 읽어보려 한다.
그 시작은 Pose Estimation Task에 처음으로 딥러닝 모델을 적용한 논문인 DeepPose이다. 나온지 10년이 된 논문이기에 핵심적인 부분만 빠르게 읽어보도록 하겠다.
0. Abstract
본 논문은 DNN(Deep Neural Network) 기반의 Regression 문제로 Pose Estimation을 해결하려 하였다.
※ Cascade : 영어로 작은 폭포라는 뜻으로 모델이 연속해서 이어진것으로 생각
1. Introduction

Human Pose Estimation은 Human Joint를 Localization(해당 Joint가 어디에 위치하는지 찾는 것)하는 문제로 정의된다. 최근 몇년 간 Part-based 모델이 다양하게 제안되었지만, 이는 표현력이 제한된다는 문제점이 있었다(Local Detector를 사용하거나 Body part의 모든 Interaction 중 일부만 모델링하여).
따라서 본 논문에서는 DNN(Deep Neural Network)을 기반으로 한 모델을 제안한다. Pose Estimation을 Joint Regression으로 공식화 하고 이를 DNN에 적용하였다. 이러한 방식은 2가지 장점이 존재하는데 첫째는 DNN이 Body Joint의 전체적인 Context를 고려한다는 점이고, 두번째는 Graphical Model보다 공식화가 단순하다는 점이다. Feature Representation이나 Detector, 모델의 Topology와 Joint간의 Interaction을 디자인할 필요가 없기 때문이다.
대신 Convolutional DNN을 사용하여 Pose Estimation을 가능케하는 Regressor를 학습하였으며 여러 Benchmark에서 우수한 성능을 보였다.
※ Part-based models : 이미지의 다양한 부분을 별도로 사용하여 관심 객체가 존재하는지 여부와 위치를 파악하는 모델
※ Articulation : 관절구조가 있는 모델을 모델링하는 것(관절화)
2. Related Work
Pose Estimation Task에서는 사람의 자세를 여러 부분으로 이루어진 그래프로 표현한 방식이 많이 등장해왔다. 특히 PS(Pictorial Structures) 기반의 다양한 모델들이 개발되었는데, 하지만 이러한 대부분의 연구는 모델의 표현력이 다소 부족했다.
따라서 Holistic한 방법으로 자세를 추론하는 연구가 계속되었고, 실용성과 표현력 두마리 토끼를 모두 잡기 위한 연구가 계속해서 이어져 왔다.
※ Pictorial Structures : 컴퓨터 비전에서 물체(사람)의 모습을 모델링하는 기법. 물체를 여러 개의 부분(part)로 나누고 이들 사이의 위치와 관계를 모델링하여 관절의 위치를 추정함. Felzenszwalb와 Huttenlocher가 거리변환(Distance Transform)을 사용해 PS 모델의 계산을 효율적으로 만듦.
https://www.cs.cornell.edu/~dph/papers/pict-struct-ijcv.pdf
3. Deep Learning Model for Pose Estimation
- $k$개의 신체 관절 위치를 포함하는 Pose Vector : $y = (y_1^T, y_2^T, ... , y_i^T)^T \quad i={1, ..., k}$
- $y_i = (x_i, y_i)$
- x는 이미지 데이터, y는 Ground Truth Pose Vector
$$N(y_i;b) = \begin{pmatrix} 1/b_w& 0\\ 0& 1/b_h\\ \end{pmatrix}(y_i - b_c)$$
- 관절 좌표가 이미지의 절대 좌표 -> 사람을 감싸는 $b$로 정규화하는 것이 유용
- $b_c$ : 박스 중심
- $b_w$ : 박스 width
- $b_h$ : 박스 height
- 위 수식은 관절 $y_i$를 박스 중심으로 이동시키고 박스 크기로 스케일링한 정규화 식
- 이러한 정규화를 Pose Vector에 적용
- $N(x;b)$ : $b$ 박스에 의해 이미지 $x$를 잘라낸 것(이미지 $x$를 $b$ 박스에 의해 정규화)
- $N(\cdot)$$b$가 전체 이미지 박스인 경우의 정규화

3.1. Pose Estimation as DNN-based Regression
본 논문에서는 Pose Estimation 문제를 Regression으로 풀며 $\psi(x;\theta) \in \mathbb{R}^{2k}$ 함수를 학습하고 사용한다.
$\theta$ : 모델 파라미터
위의 정규화 표현식을 사용하여 절대 이미지 좌표계에서 포즈를 예측한 $y^*$는 아래와 같다.
$$y^* = N^{-1}(\psi(N(x); \theta))$$
DNN 기반의 함수인 $\psi$가 중요한 역할을 하며 Convolution, LRN(Local Response Nomalization), Pooling, Fully Connected Layer가 결합한 7개의 층으로 구성되어 있다.
C1(55x55x96) - LRN - P - C2(27x27x256) - LRN - P - C3(13 x 13 x 384) - C4(13 x 13 x 384) - C5(13 x 13 x 256) - P - F(4096) - F(4096)
DNN을 사용함으로써 특정 도메인에 맞게 Pose Model을 설계할 필요가 없고, 관절 간의 Interaction을 모델링하지 않아도 된다. C1은 11x11, C2는 5x5 크기의 필터를 사용하며 나머지 3개의 Convolution layer에서는 3x3 크기의 필터를 사용한다.
Training
본 논문에서는 네트워크의 마지막 층에 Linear Regression을 적용하여 예측한 Pose Vector와 실제 Pose Vector간의 L2 거리를 최소화하는 방식으로 모델을 학습하였다. 이 때 실제 Pose Vector는 절대 이미지 좌표계로 정의되기 때문에 앞서 소개한 정규화를 사용한다.
LeNet 모델과 비슷한 Convolution + Fully Connected 구조로 Pose Estimation을 수행한다.
3.2. Cascade of Pose Regressors
3.1.에서 나타난 Pose Formulation의 장점은 Pose Estimation이 전체 이미지를 기반으로 이루어진다는 것이다. 하지만 입력 크기가 220x220으로 한정되어 네트워크가 Detail을 보는데에 한계가 존재한다.
따라서 본 논문에서는 Pose Estimator를 연속해서 학습시키는 Cascade 방법을 제안한다. Figure 2에 보이는 것처럼 첫번째에는 Initial Pose를 추정하고, 점차 단계를 거쳐가며 현재 예측한 Joint의 위치를 정밀하게 조정해간다. 이 때 이전 단계에서 예측된 관절 위치 주변의 이미지를 자르고 해당 이미지에다가 Pose Displacement Regressor를 적용한다. 이를 통해 이후의 Pose Estimator는 더 높은 해상도의 이미지를 보고 더 디테일한 특징을 파악할 수 있어진다.
Cascade의 모든 단계에서 동일한 아키텍처를 사용하지만 단계별로 다른 네트워크 파라미터를 학습한다. S개의 Cascade 단계 중 s 단계의 네트워크 파라미터는 $s_{\theta}$로 나타낸다. 또한 주어진 관절 위치 $y_i$를 조정하기 위해 관절 주변의 Bounding Box $b_i$를 고려하는데, 이 때 Bounding Box는 $b_i(y;\sigma) = (y_i, \sigma \cdot diam(y) \cdot diam(y))$이며 중심은 $i$번째 관절, 크기는 $\sigma$로 조정된 $diam(y)$이다. 자세의 지름을 뜻하는 $diam(y)$는 인체의 몸통에서 대각선으로 마주보는 관절의 거리를 의미한다.
$\sigma$ : Bounding Box 크기를 정의하는 비율(Scaler)
첫번째 단계에서는 전체이미지를 넣은 $b_0$으로 시작하여 초기 자세를 생성한다. 이후 2번째 단계부터는 이전 단계에서 정의된 하위 이미지에 대해 회귀 모델을 적용하여 변위와 새로운 관절박스를 추정한다.
Training
네트워크 파라미터는 L2 Loss에 의해 학습된다. 이 때 중요한 점은 각 관절 $i$가 이전 단계에서 동일한 관절에 대해 얻은 예측값을 중심으로한 Bounding Box를 사용하여 정규화한다는 점이다. 학습 과정 도중 이미지와 관절에 대해 여러가지 정규화를 사용하여 학습 데이터를 증강하여 사용하기도 하였다.
4. Empirical Evaluation
사용한 데이터
- FLIC(Frames Labeled In Cinema) : 4000 Train Image / 1000 Test Image, 10 Upper Body Joints
- LSP(Leeds Sports Dataset) + Extension : 11000 Train Image / 1000 Test Image, 14 Full Body Joints
- 두 데이터 모두 Shoulder와 반대편 Hip까지의 거리를 $diam(y)$로 정의
Metric
- PCP(Percentage of Correct Parts) : Detection rate of limbs. 짧은 팔다리에 penalizing하기 어려움
- PDJ(Percent of Detected Joints) : PCP의 단점 보완. 예측한 관절 위치와 실제 관절 위치 사이 거리가 Diameter의 일정 비율 이내일때 해당 관절이 검출된 것으로 간주
Experimental Detail은 논문 원본을 참고
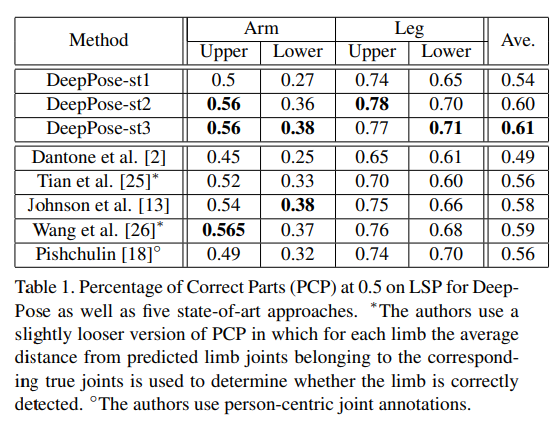
LSP 데이터 셋에 대해 PCP 평가지표를 적용한 결과. 가장 판단이 어려운 팔과 다리의 상하부 추정 성능을 비교하였으며 DeepPose 모델이 모든 부위에서 고르게 좋은 성능을 낸 것을 확인할 수 있다.

FLIC 데이터 셋에 대해 PDJ 평가지표를 적용한 결과이다. DeepPose가 기존 모델들 대비 좋은 성능을 보였다.

위 실험은 Cascade 구조의 효용성을 알아보는 실험이다. 초기 예측과 두번째, 세번째 단계의 Presicion을 비교한 결과 뒤의 Stage로 갈 수록 성능이 많이 개선되는 것을 확인할 수 있다.
이뿐만 아니라 LSP와 FLIC로 학습한 모델을 ImageParse, Buffy 데이터 셋에도 적용해 보았는데 좋은 성능이 보이는 것을 확인할 수 있었다. 이를 통해 알고리즘의 우수한 일반화 능력을 입증하였다.
처음으로 Pose Estimation Task에 딥러닝을 적용하였다는 것 말고도 Cascade 구조로 원하는 Joint의 주변 부분을 같이 학습에 녹였다는 점이 중요한 Contribution으로 나타나는 논문이라고 생각한다. Top-Down과 Bottom-Up에 대한 명확한 구분이 없었기에 Input이 꼭 사람 Bounding Box가 아닌 이미지 전체가 들어가는 케이스 또한 고려가 된, 정말 초창기 Pose Estimation의 연구 형태를 확인할 수 있었던 논문이었다. 사용하는 데이터도 평가지표도 최근 논문과는 거리가 멀지만 해당 시점에 Pose Estimation 문제를 풀기 위해 어떤 방식으로 접근하였는지를 느낄 수 있었다는 점에 또다른 Contribution을 주고싶다.
세 줄 요약
1. 전체 이미지 Context를 모델링하기 위해 Pose Estimation 분야에 딥러닝 모델을 적용함
2. 간단한 Convolution + FC Layer 구조와 Cascade 구조를 통해 모델이 이미지의 Detail을 학습하도록 설계하였다(표현력 + 효율성).
3. LSP, FLIC 데이터에서 좋은 성능을 보였고 방법론에 대한 성능 증명, 크로스 데이터 검증 등의 실험을 진행하였다.

'논문 paper 리뷰' 카테고리의 다른 글
| [Paper Review] Stacked Hourglass 논문 이해하기 (0) | 2024.09.03 |
|---|---|
| [Paper Review] ViTPose 논문 이해하기 (1) | 2024.08.30 |
| [Paper Review] MIPNet 논문 이해하기 (0) | 2024.08.28 |




댓글