『 HybrIK: A Hybrid Analytical-Neural Inverse Kinematics Solution for 3D Human Pose and Shape Estimation. CVPR. 2021. 』
- 최근 Pose 관련 여러 논문을 읽었지만 차분히 논문을 정리할 시간이 부족해 리뷰를 작성하지 못했던 것 같다. 따라서 이번 리뷰를 시작으로 다시 논문 리뷰를 꾸준히 작성해 보려한다.
- 본 논문은 3D Human Pose 분야의 논문으로 하나의 Monocular RGB 카메라로 촬영한 이미지를 가지고 3D Mesh를 만드는 새로운 모델인 HybrIK를 소개한다.
- 관련 3D Mesh 모델의 기본이 되는 SMPL에 대한 공부가 선행되어야 좋으며 해당 논문은 추후에 리뷰하도록 하겠다.
0. Abstract
Model-based 3D pose & shape는 몇 가지 파라미터를 추정하여 사람의 3D Mesh를 재구성한다. 하지만, 파라미터를 추정하는데 있어 misalignment 문제나 모델 성능에 따라 그 성능이 달라진다는 문제점이 존재한다. 한편 3D Keypoint Estimation은 pixel-level의 localization accuracy를 목표로 하지만 실제와 다른 신체 구조를 예측할 수 있다는 단점이 존재한다.
따라서 본 논문에서는 Body Mesh Estimation과 3D Keypoint Estimation의 간극을 줄인 HybrIK(Hybrid Inverse Kinematics Solution) 모델을 제안한다. 이 모델은 twist-swing decomposition을 통해 정확한 3D 좌표로부터 상대적인 Rotation을 얻어낸다. 이 때 twist rotation은 Neural Network에서 얻어낸 시각적인 정보에서 얻어낸다.
Model-Based vs Model-Free
(1) Model-based: 사전에 정의된 모델을 사용하여 입력 데이터로부터 3D Mesh를 생성. 이미 존재하는 구조를 따르기 때문에 정확도와 일관성에 있어 강점을 가지지만, 일반적이지 않은 데이터가 들어올 경우 잘 처리하기 어렵다.
(2) Model-free: 사전에 정의된 모델 없이 데이터에서 직접 3D Mesh를 생성하는 방식으로 주로 딥러닝 모델을 활용. 딥러닝 네트워크가 데이터를 바로 3D Mesh로 변환하는 방법을 학습하기 때문에 유연성이 강점이지만, 많은 학습 데이터가 필요하다는 점, 결과에 대한 설명력이 부족하다는 등의 단점을 가진다.
1. Introduction
Monocular RGB image에서 3D surface를 추정하는 문제는 ill-posed problem(해결방법이 유일하지 않은 문제)이다. 대표적인 Parametric Statistical Human Shape Model인 SMPL, SMPL-X의 발달으로 몇가지 파라미터만 가지고도 실제와 비슷하고 컨트롤 할 수 있는 3D Mesh를 만들어낼 수 있게 되었다(ex. 여기서 몇가지 파라미터는 Shape, Relative Rotation parameter 등). 최근 SMPLify, HMR, SPIN과 같은 Model-based 모델들이 하나의 Monocular RGB Image에서 파라미터를 얻어내고 3D Pose와 Shape를 만들어 낸다.
Model-based 방법론에는 크게 Optimization-based와 Learning-based 기법이 존재한다.
Optimization-based Approach
[대표적인 모델: SMPLify, SMPLify-X]
: 반복적인 Fitting process를 통해 body pose & shape parameter를 예측한다. 이 때 파라미터들은 예측된 2D 좌표와 실제 2D 좌표간의 error를 줄이도록 조정되었다. 단점으로는 optimization 과정이 non-convex하고 오래걸린다는 점이며 이러한 점을 개선하기 위해 Learning-based Approach가 등장하였다.
Learning-based Approach
[대표적인 모델: HMR, SPIN, Vibe]
: Direct하게 모델 파라미터를 예측(regress)하기 위해 Neural Network를 사용한다. 하지만 통계 모델의 매개변수 공간은 추상적이어서 네트워크가 매핑 함수를 학습하기가 어렵다.
이러한 문제점들 때문에 본 논문에서는 3D Keypoint Estimation 분야에 주목하였다. 위의 방법론들의 문제점을 개선하기 위해 Direct한 Regression 대신 3D joint 위치에 대한 Volumetric Heatmap을 학습하는 방법론을 제안한 몇몇 연구(ex. C2F, Integral Human Pose Regression)가 존재하는데, 본 논문에서는 해당 모델들에서 영감을 받아 3D Joint와 Body Mesh간의 Collaboration을 만들고자 하였다.
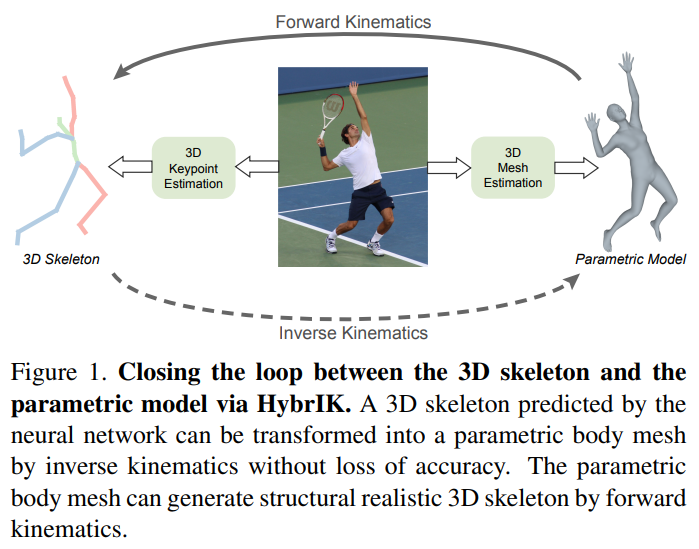
본 논문의 저자들은 기존의 Shape 파라미터를 사용하는 것이 정확하게 예측한 3D Joint를 Mesh 형태로 만들 때 unrealistic한 Body Structure를 예측한다고 생각한다. 따라서 Inverse Kinematics Process를 활용하여 3D Keypoint Estimation과 Body Mesh Estimation의 gap을 줄인 HybrIK 모델을 제안한다. IK(Inverse Kinematics) process는 Body Joint의 바람직한 위치를 찾기 위한 Relative Rotation을 구하는 방법으로 twist-and-swing decomposition을 통해 이를 구현한다.
Relative Rotation -> twist(종방향 회전), swing(횡방향 회전)
HybrIK에서는 swing 회전과 twist 회전을 예측함으로써 Kinematic Tree에 따라 전체 회전을 재귀적으로 합성한다. 이 때 별도의 optimization 과정 없이 Relative Rotation을 예측할 수 있다. 모든 HybrIK 연산은 미분 가능하기 때문에 3D Joint와 Mesh를 한번에 End-to-End로 학습할 수 있다.
Kinetic : 움직임을 발생시키는 힘에 대한 분석
Kinematic : 움직임에 영향을 미치는 힘을 고려하지 않고 움직임의 형태만 분석
2. Related Work
3D Keypoint Estimation
지금까지의 3D Keypoint Estimation은 2가지 방법으로 나뉜다.
(1) Single-stage
: Input 이미지에서 바로 3D Joint의 위치를 예측하는 방법. 3D heatmap, location-map, 2D heatmap + regression 방법론이 존재한다.
ex. C2F, Lcr-net, HMOR 등
(2) Two-stage
: 2D pose를 먼저 예측한 뒤 이미 학습된 2D-3D skeleton dictionary에 따라 변환 or 2D 좌표를 3D 좌표에 Regression. 2D Pose를 정확하게 잡아내는 것이 중요하다.
Model-based 3D Pose and Shape Estimation
Model-based 3D Pose and Shape Estimation 방법론은 Parametric Human Body Model을 사용해왔다(SCAPE, SMPL, SMPL-X). 여기에 더하여 딥러닝의 발달과 함께 학습 기반의 방법론이 발전하였고 하나의 RGB 이미지에서 shape space와 Relative Rotation을 매핑하는 것이 어렵기 때문에 keypoint, segmentation, 2D heatmap 등 이를 보완하는 여러 방법론들이 등장하였다.
예를들어 HMR에서는 adversarial prior와 iterative error feedback(IEF)을 통해 regression의 어려움을 줄였고, Vibe와 같이 temporal context를 이용하거나 SPIN처럼 최적화 패러다임을 적용하여 Unlabeled Image에 추가적인 3D Supervision을 제공하기도 하였다.
Body-part Rotation in Pose Estimation
Deep kinematic pose regression : 네트워크를 사용하여 각 신체 관절의 회전 각도를 예측한 다음 FK layer를 사용하여 3D 관절 좌표를 생성
Xnect : 3D 관절을 먼저 추정한 후 fitting 절차를 통해 Rotation Euler 각도를 찾음.
하지만 이전의 접근 방식들은 학습하기 어렵거나 추가적인 fitting 절차가 필요하기 때문에 본 연구에서는 hybrid IK Process를 사용하여 3D Joint Location에서 직접적이고 정확하게 Rotation을 뽑아냄
Inverse Kinematics Process
Inverse kinematics 문제에 대한 연구가 최근 많이 진행되고 있다. 시간이 오래걸리는 iterative optimization 문제가 있는 Numerical solution, 각 iterative마다 낮은 계산 비용을 가지는 Heuristic 방법 등이 있으며 최근에는 신경망을 사용하여 IK 문제를 해결하려는 여러 시도가 존재한다.
본 연구에서는 분석 솔루션의 해석 가능한 특성과 신경망의 유연성을 결합한 Hybrid IK 알고리즘을 소개한다. 이 알고리즘의 기반이 되는 기법은 twist-and-swing decomposition이며 신경망에 의해 추정되는 twist 각도는 모든 신체 관절에 대해 일반화될 수 있다.
3. Method
3.1. Preliminary
Forward Kinematics
: T-Pose와 Relative Rotation을 통해 움직인 관절의 좌표를 추정
$$Q = FK(R, T)$$
$Q = \{q_k\}^{K}_{k=1}$
$T = \{t_k\}^{K}_{k=1}$
$R = \{R_{pa(k), k}\}^{K}_{k=1}$
$K$ : Body Joint의 개수
$q_k$ : k번째 Joint의 재구성된 3D 위치
$t_k$ : Rest Pose(T-pose)에서 k번째 Joint의 위치
$pa(k)$ : k번째 Joint의 Parent Joint 인덱스
$R_{pa(k), k}$ : Parent Joint에 대한 k번째 Joint의 상대적인 Rotation
$$q_k = R_k(t_k - t_{pa(k)}) + q_{pa(k)}$$
: FK는 Root Joint부터 Leaf Joint까지 재귀적으로 Rest Pose를 회전시키며 수행된다.
$$R_k = R_{pa(k)}R_{pa(k), k}$$
$R_k$ : 표준 Rest Pose에 대한 k번째 Joint의 Global Rotation
Parent Joint가 없는 Root Joint에 대해서는 $q_0 = t_0$이다.
Inverse Kinematics
: 관절 좌표와 T-Pose를 통해 Relative Rotation을 구하는 과정
$$R = IK(P, T)$$
$p_k$ : 관절 좌표의 K번째 Joint
$$p_k - p_{pa(k)} = R_k(t_k - t_{pa(k)})$$
: 결과 Rotation이 따르는 조건식
FK와 비슷하게 $p_0 = t_0$인 루트 Joint는 Parent Joint가 없으며 IK문제는 Solution이 없거나 무수히 많은 ill-posed 문제이다.
SMPL Model
본 연구에서는 Human Body Representation을 위해 SMPL 모델을 사용하였다. Shape 파라미터로는 Shape Space의 주성분 Top10, Pose 파라미터로는 23개의 Joint의 Relative 3D Rotation 값이다. 두 가지 파라미터를 이용해 SMPL에서는 6980개의 Vertex를 생성하고, 이후 FK 과정을 통해 3D Joint를 추정한다.
3.2. Hybrid Analytical-Neural Inverse Kinematics
Relative Rotation에서 바로 Body Mesh를 예측하는 것은 매우 어려운 문제이다(HMR, Vibe, SPIN). 따라서 본 논문에서는 3D Keypoint Estimation을 활용하여 3D Body Mesh를 강화하는 HybrIK(hybrid analytical-neural inverse kinematics solution)를 제안한다. 3D Joint는 Relative Rotation을 결정할 수 없기 때문에 Rotation을 Twist와 Swing으로 나누었고, 3D Joint는 Swing Rotation을 계산하는데 사용되며, 신경망을 통해 1-DoF인 Twist Rotation을 추정한다. 이 때 Relative Rotation은 Kinematic Tree를 따라 재귀적으로 계산한다.
Twist-and-Swing Decomposition

Analytical IK formulation에서 몇몇 Body Joint들은 문제를 단순화하기 위해 자유도를 낮춘다. 하지만 본 연구에서는 각각의 Body Joint는 모두 3의 자유도를 가진다고 가정하였고, 이를 twist와 swing rotation으로 분해하였다. Template Body Vector인 $\vec{t}$와 Target Vector인 $\vec{p}$에 대해 Solution Process인 $R$은 다음과 같이 정의된다.
$$R = \mathcal{D}(\vec{p}, \vec{t}, \phi) = \mathcal{D}^{sw}(\vec{p}, \vec{t})\mathcal{D}^{tw}(\vec{t}, \phi) = R^{sw}R^{tw}$$
$\phi$ : twist 각도(Neural Network를 통해 예측)
$\mathcal{D}^{sw}(\cdot)$ : swing rotation의 closed-form solution
$\mathcal{D}^{tw}(\cdot)$ : $\phi$를 twist rotation으로 바꾸는 함수
여기서 $R$은 $\vec{p} = R\vec{t}$ 방정식을 만족해야 함(목표 포즈 = 회전·T-pose)
(1) Swing
Swing Rotation은 $\vec{t}$와 $\vec{p}$에 수직인 axis $\vec{n}$을 갖는다.
$$\vec{n} = \frac{\vec{t}\times\vec{p}}{\left\|\vec{t}\times\vec{p}\right\|}$$
이 때 Swing angle인 $\alpha$는 다음의 식을 만족한다.

따라서 closed-form solution인 swing rotation $R^{sw}$는 Rodrigues formula에 의해 얻어진다.
$$R^{sw} = \mathcal{D}^{sw}(\vec{p}, \vec{t}) = \mathcal{I} + sin\alpha[\vec{n}]_{\times} + (1-cos\alpha)[\vec{n}]^2_{\times}$$
$[\vec{n}]_{\times}$ : $\vec{n}$의 skew symmetric matrix($-A$=$A^T$ 인 행렬)
$\mathcal{I}$: 3x3 단위행렬
※ Rodrigues Formula
: Axis와 Angle이 주어졌을 때 특정 벡터를 해당 Axis에 대해 해당 Angle만큼 회전시킨 벡터를 구하는 공식 (Rotation Matrix를 구할 때 사용)
어떻게 됐든 타겟 포즈와 T-Pose 벡터를 가지고 swing rotation을 얻을 수 있었다는 내용
(2) Twist
$\vec{t}$ 자신을 축 기준으로 잡고 $\phi$ 각도를 알면 twist rotation $R^{tw}$를 정의할 수 있다.
$$R^{tw} = \mathcal{D}^{tw}(\vec{t}, \phi) = \mathcal{I} + \frac{sin\phi}{\left\| \vec{t} \right\|}[\vec{t}]_{\times} + \frac{(1-cos\phi)}{\left\| \vec{t} \right\|}^2[\vec{t}]^2_{\times}$$
$[\vec{t}]_{\times}$ : $\vec{t}$의 skew symmetric matrix
$\mathcal{D}^{sw}$ & $ \mathcal{D}^{tw}$ : 모두 미분가능
twist angle은 1-DoF 변수이며 변화량이 작다. 따라서 Network에서 mapping function을 학습하기 더 편하다.
기존 Learning Based Approach의 단점인 Mapping Function을 학습시키기 어렵다는 점이 보완됨
Naive HybrIK

IK Process는 FK Process 처럼 Kinematic Tree를 따라 재귀적으로 수행된다.
- Global Root Rotation $R_0$을 결정(Spine, left hip, right hip을 SVD하여 계산)
- Parent Joint인 $R_{pa(k)}$를 알고있다고 가정하며 매 k번째 step은 다음의 식을 따른다.
$$R^{-1}_{pa(k)}(p_k - p_{pa(k)}) = R_{pa(k), k}(t_k - t_{pa(k)})$$이 때 $\vec{p}_k = R^{-1}_{pa(k)}(p_k - p_{pa(k)})$와 $\vec{t}_k = (t_k - t_{pa(k)})$로 두면 Relative rotation은 다음과 같이 구할 수 있다.$$R_{pa(k), k} = \mathcal{D}(\vec{p}_k, \vec{t}_k, \phi_k)$$$\phi_k$ : 네트워크를 통해 예측한 k번째 Joint의 twist angle
Rotation Matrix는 Orthogonal하기 때문에 역행렬과 전치행렬이 같다. 따라서 미분 가능하다. 여기서 Global Rotation $R_k$ 대신 Relative Rotation인 $R_{pa(k), k}$으로 계산하는 것은 만약 Global Rotation을 바로 분해할 경우 twist angle이 kinematic tree에 따라 모든 상위 rotations에 의존하기 때문이다(학습이 어려워짐).
Adaptive HybrIK

$$\left\|p_k = p_{pa(k)}\right\| = \left\|t_k = t_{pa(k)}\right\|$$
Naive HybrIK는 위와 같은 가정을 따르는데, 이 때 3D Keypoint Estimation으로 추정된 결과가 항상 T-pose template과 일치하지는 않는다. 따라서 이 때 발생하는 오류를 보정하기 위해 Reconstruction error $\vec{\epsilon}_k$을 사용한다. 이 때 식은 아래와 같다.
$$p_k - p_{pa(k)} = R_k(t_k - t_{pa(k)}) + \vec{\epsilon}_k$$
이 때 FK가 반복되면서 오차항은 반복되며 누적되는데 이 경우 말단 Joint에 대한 불확실성이 커진다. 본 논문에서는 이러한 문제를 해결하기 위해 Adaptive HybrIK를 제안한다.

왼쪽의 그림을 보면 본래의 Target Direction을 맞추기 위해 step마다 Error가 누적되는 것을 확인할 수 있다. 따라서 Adaptive HybrIK에서는 매 step마다 현재의 Joint에만 집중할 수 있도록 target direction을 이전의 예측값-다음 정답값으로 변경한다. 따라서 수식은 다음과 같이 바꿀 수 있다.
3.3. Learning Framework
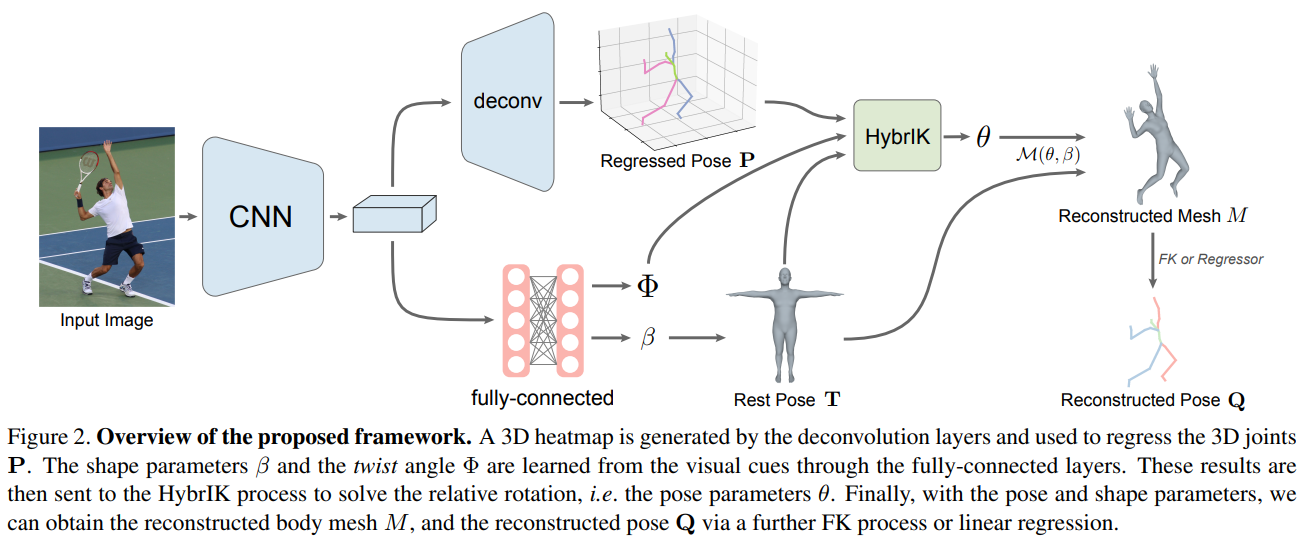
전체적인 Framework는 Figure 2와 같으며 모든 과정은 미분가능하고 End-to-End 학습이 가능하다.
- 3D Joint P, twist angle $\Phi$, shape parameter $\beta$를 찾기 위해 Neural Network를 사용
- Shape parameter $\beta$와 SMPL 모델을 이용해 rest pose T를 얻음
- P, T, $\Phi$를 가지고 HybrIK 모델을 돌려 relative rotation R을 계산(pose parameter $\theta$)
- SMPL 모델을 이용해 $\mathcal{M}(\theta, \beta)$를 풀어 mesh $M$을 얻어냄
- 이 때 재구성된 pose Q는 mesh M에서 FK 과정을 통해 얻을 수 있음
3D Keypoint Estimation
본 논문에서는 3D body keypoint를 추정하기 위해 간단하지만 효과적인 구조를 활용하였다. Backbone으로 ResNet을 사용하였고 Heatmap을 만들기 위한 3개의 Deconv + 1x1 Conv layer가 뒤를 잇는다.
얻어낸 Heatmap에서 3D Pose를 찾아내기 위해 soft-argmax를 사용하며 이 때 Loss는 L1 Loss를 사용한다.
$$\mathcal{L}_{pose} = \frac{1}{K}\sum_{k=1}^{K}\left\|p_k - \hat{p}_k\right\|_1$$
$\hat{p}_k$ : ground-truth joint
Twist Angle Estimation
Discontinuity 문제를 피하기 위해 Scalar value인 $\phi_k$를 바로 regression하는 대신 본 논문에서는 2차원 벡터인 $(c_{\phi_k}, s_{\phi_k})$를 학습한다($cos\phi, sin\phi$). Loss는 L2 Loss를 따른다.
$$\mathcal{L}_{tw} = \frac{1}{K}\sum_{k=1}^{K}\left\|(c_{\phi_k}, s_{\phi_k}) - (cos\hat{\phi}_k, sin\hat{\phi}_k)\right\|_2$$
$\hat{\phi}_k$ : ground-truth twist angle
Collaboration with SMPL
SMPL 모델을 Shape Parameter $\beta$에 따라 Additive Offset이 있는 Rest Pose Skeleton을 얻을 수 있다.
$$T = W(\overline{M}_T + B_S(\beta))$$
: 주어진 Shape에 $\beta$에 대한 Blend shape를 계산한 결과(Offset)을 더해서 Rest Pose T를 구함
학습과정에서 shape parameter와 rotation parameter의 Loss는 다음과 같다.
$$\mathcal{L}_{shape} = \left\|\beta - \hat{\beta}\right\|_2$$
$$\mathcal{L}_{rot} = \left\|\theta- \hat{\theta}\right\|_2$$
따라서 전체 Loss는 다음과 같다.
$$ \mathcal{L} = \mathcal{L}_{pose} + \mu_1\mathcal{L}_{shape} + \mu_2\mathcal{L}_{rot} + \mu_3\mathcal{L}_{tw}$$
이 때 $\mu_1$ = 1, $\mu_2$ = $\mu_3$ = 1 X $10^{-2}$
3.4. Implementation Details
Network Backbone : ResNet-34
ResNet의 output을 2 branch로 나누어서 하나는 3D Heatmap를 생성하고 하나는 Average Pooling -2 FC layer (Dropout) - FC layer로 구성된다.
Input Image : 256 x 192로 Resize
Learning Rate : 0.001로 시작, 90번째에 0.0001, 120번째에 0.00001로 줄임
Optimizer : Adam
Epoch : 140
Batch Size : 8 GPU x 32 batch size
참고자료
https://jhtobigs.oopy.io/77a5c52a-3ef4-4ece-bc14-99fce1469011
리뷰 : HybrIK
A Hybrid Analytical-Neural Inverse Kinematics Solution for 3D Human Pose and Shape Estimation 리뷰
jhtobigs.oopy.io
세 줄 요약
1. HybrIK는 3D Joint, Twist angle, Rest Pose를 가지고 Pose parameter를 구한 뒤 Shape & Pose parameter를 이용하여 3D Mesh를 구하고 그렇게 구한 3D Mesh를 FK를 통해 3D Joint를 예측하는 과정을 학습한 모델이다.
2. 이 때 3D Joint에서 바로 Relative Rotation을 계산하기 어렵기 때문에 Swing(3D Joint, Rest Pose) & Twist Rotation(Rest Pose, Twist angle)으로 분해
3. 본 논문에서 SMPL은 Rest Pose T를 구할 때, 3D Mesh Vertex를 구할 때 사용된다.

'논문 paper 리뷰' 카테고리의 다른 글
| [Paper Review] HRNet for Visual Recognition 논문 이해하기 (0) | 2024.03.24 |
|---|---|
| [Paper Review] METER 논문 이해하기 (0) | 2023.11.04 |
| [ToBig's] BERT 논문 이해하기 (0) | 2023.09.13 |




댓글