『 VAE : Auto-Encoding Variational Bayes. 2014. 』
사전 지식
※ MLE (Maximum Likelihood Estimation)
MLE는 어떤 상황이 주어졌을 때, 해당 상황을 가장 높은 확률로 산출하는 후보를 선택하는 방법을 말한다 (주어진 데이터셋이 나올 확률을 최대로). 예를들어 땅에 떨어진 머리카락을 발견했을 때 이것이 남자의 머리카락인지 여자의 머리카락인지 판단하는 Task가 있다고 해보자, 이 때 우리는 성별별 머리카락 길이의 일반적인 확률분포를 떨어진 머리카락의 길이와 비교하여 성별을 판단하는 추론을 진행할 수 있다.
※ MAP (Maximum A Posterior)
MLE가 Likelihood를 최대화 시키는 방법이었다면, MAP는 Posterior를 최대화 시키는 방법이다. 이 때 일반적인 추론 상황에서는 사후 확률 분포가 존재하지 않기 때문에 베이즈 정리를 이용한 추론을 진행한다.
※ 베이즈 정리
$$ P(A|B) = \frac{P(B|A)P(A)}{P(B)} $$
A : 구하려는 대상 / B : 주어진 대상(관측 값)
Prior : $P(A)$, 구하려는 대상 자체의 확률
Likelihood : $P(B|A)$, 구하려는 대상이 주어졌을 때, 해당 관측 값이 나올 확률
Posterior : $P(A|B)$, 관측 값이 주어졌을 때, 구하려는 대상이 나올 확률
Ex. 머리카락의 길이를 보고 성별 예측
주어진 대상 : 머리카락(길이)
구하려는 대상 : 성별(남/여)
Prior = P(남자) or P(여자)
Likelihood = P(머리카락|남자) or P(머리카락|여자)
Posterior = P(남자|머리카락) or P(여자|머리카락)
$$ P(남자|머리카락) = \frac{P(머리카락|남자)P(남자)}{P(머리카락)} $$
이 경우 문제를 풀 때, Likelihood를 최대화하는 MLE 방식은 P(머리카락|남자) or P(머리카락|여자) 두 Likelihood를 비교하여 둘 중 큰 값을 선택한다.
반대로 MAP 방식은 두 Posterior를 비교해서 둘 중 큰 값을 선택하는데, 이 때 처음부터 Posterior를 알기는 어렵기 때문에 베이즈 정리를 활용해 계산한다. 하지만 사전확률을 구하는게 어렵기 때문에 현실에서는 MLE를 쓸 때도 많다.
Ex 2. 영상에서 피부색을 검출하는 문제
영상에서 피부색을 검출하는 문제는 각 픽셀 별로 피부색에 해당하는지 아닌지 여부를 결정하는 분류 문제로 볼 수 있다. 하지만 이 때 MAP 방식을 사용한다면, P(피부색)에 대한 Prior 확률이 필요한데 우리가 수집한 데이터 만으로 세상에 있는 피부색 확률이라고 추정할 수 없다.
이런 경우에는 MLE 방법을 사용해야 한다.
<참고자료>
https://aimaster.tistory.com/79
https://hwiyong.tistory.com/27
http://darkpgmr.tistory.com/62
자, 그럼 논문과 비교해가며 VAE 모델을 이해해 보도록 하자 (〜 ̄▽ ̄)〜
0. Abstract
본 논문에서는 다루기 힘든(Intractable) 사후 분포를 가지는 연속적인 Latent Variable과 대규모 Dataset에 대해 Directed Probabilistic Model으로 효율적으로 추론하고 학습시키는 Stochastic Variational Inference & Learning Algorithm을 제안하였다.
이 알고리즘은 크게 2가지에 기여한다. 우선 첫째로는 Variational Lower Bound의 Reparameterization으로 확률적 경사 방법들(Standard Stochastic Gradient Method)을 사용해 최적화할 수 있는 Lower Bound Estimator를 만든다는 것이다.
두번째는 각 Datapoint가 연속적인 Latent Variable를 가지는 i.i.d. Dataset에서 Approximate Inference Model(= recognition model)을 위에서 제안한 Lower Bound Estimator를 사용한 다루기 힘든 사후분포에 fitting함으로써 사후 추론을 효율적으로 진행할 수 있다.
※ i.i.d. (independent and identically distribution)
: 독립항등분포, 각 사건이 다른 사건에 영향을 주지 않고 각 사건이 동일한 분포를 따름
1. Introduction
Introduction에서는 Abstract를 바로 읽으면 잘 이해가 되지 않기 때문에 더 자세히 풀어서 설명해준다.
연속적인 Latent Variable과 Parameter가 다루기 힘든 사후분포를 갖는 Directed Probabilistic Model을 사용해서 어떻게 효율적으로 Approximate Inference를 할 수 있을까?
※ Latent Variables
잠재 변수란 관측 가능한 데이터와 관련은 있지만 직접적으로 측정되지 않는 변수를 의미한다. 일반적으로 데이터에서 패턴을 발견하거나 결과를 예측하는 데 사용되며, 잠재 변수를 사용하면 데이터의 차원을 줄일 수 있다.
그럼 Continuous Latent Variable은 무엇일까?
연속 잠재 변수는 잠재 변수의 한 유형으로 연속적인 값을 가지는 변수이다. 실수 범위 내에서 가능한 모든 값을 가질 수 있으며 주로 확률론적 모델링에서 사용된다. (ex. 주성분 분석(PCA), 요인 분석(Factor Analysis), 가우시안 혼합 모델(GMM))
기존 VB(Variational Bayesian) 접근 방식은 Intractable Posterior에 대한 Approximation의 최적화를 포함하고, SGVB(Stochastic Gradient Variational Bayes) 추정은 연속적인 Latent Variable과 Parameter를 사용하는 대부분의 모델에 대해 Approximate Posterior Inference가 가능하다. 이를 위해 미분 가능한 Variational Lower Bound의 Reparameterization을 사용한다.
결국 Datapoint 마다 i.i.d 하고 연속적인 Latent Variable일 경우, MCMC(Markov Chain Monte Carlo)같이 계산량이 많은 추론 대신 AutoEncoding VB(AEVB) 알고리즘으로 효율적인 Approximate Posterior Inference가 가능하다.
MLE 방법을 사용하든, MAP 방법을 사용하든 사전확률을 계산할 때 Latent Variable을 적분해주어야 하는데 이것은 Intractable 하다. 이를 해결할 수 있는 가장 대표적인 방법이 MCMC로, 여러 시행의 반복을 통해 확률 분포를 얻어내는 방법이다. 하지만 MCMC는 큰 데이터 셋에서 여러번의 sampling을 진행해야 하기 때문에 학습 속도가 느려지게 된다.
따라서 본 논문에서는 이 단점을 극복하기 위해 MCMC 방법이 아닌 AEVB 알고리즘을 제안한 것이다.
2. Method
※ 딥러닝 생성 모델
생성 모델은 주어진 데이터 셋과 유사하면서 새로운 데이터를 생성해 낼 수 있는 모델을 만드는 것이 목표이다. 이를 위해 확률적인 관점에서 보면 $x$라는 데이터 셋이 있을 때 확률함수 $p^*$를 거친 $p^*(x)$가 기존 데이터인 $x$와 유사해야 한다.
하지만 현실적으로 우리가 직접적인 확률함수 $p^*$를 알아내는 것은 불가능하다. 따라서 우리는 최대한 해당 함수인 $p^*$과 비슷하도록 새로운 데이터를 만들 수 있는 $p_\theta$를 만들려한다.
$$ p^{*}(x) \approx p_{\theta}(x)$$
그렇지만 아직도 $p_{\theta}(x)$를 직접적으로 알아내는 것은 Intractable하다. 따라서 VAE 모델은 몇 가지 가정 하에 생성모델을 설계하고 훈련하여 $p_{\theta}(x)$를 간접적으로 알아내는 것을 가능케한다.
[가정 1] i.i.d 가정(independent and identical distribution assumption)
우리가 만들고자 하는 데이터의 전체 집합을 $X$라고 할 때, $X$의 각 원소들을 $p_{\theta}(x)$에 의해 확률적으로 뽑는다면 각 시행은 독립적이며 동일한 분포를 가진다. (여기서 $X$는 주어진 데이터만이 아닌 주어진 데이터 분야의 모든 데이터를 말한다)
Independent : 생성모델로 어떤 이미지를 새롭게 만들 때, 이전 혹은 이후에 생성할 이미지에 영향 X
Identical : 이미지 각각은 해당 데이터 집합 $X$에 대한 이미지로, 뜬금없이 다른 $Y, Z$에 대한 이미지를 만들어내지 않음
[가정 2]
충분한 양의 학습 데이터 셋 $\{x^{(i)}\}_{i=1}^{N}$이 있을 때, 이 학습 데이터 셋은 데이터의 모집합 $X$를 어느정도 대체할 수 있다.
위의 두 가정을 통해 우리는 주어진 각 데이터에 대해 동일한 분포로부터 발생한 독립적인 사건의 곱으로 생각할 수 있다.
$$ p^{*}(X) \approx p_{\theta}(X) \approx p_{\theta}(\{x^{(i)}\}_{i=1}^{N}) = p_{\theta}(x^{(1)}, \cdots, x^{(N)}) = p_{\theta}(x^{(1)}) \cdots p_{\theta}(x^{(N)}) = \prod_{i=1}^{N}p_{\theta}(x^{(i)}) $$
2.1. Problem scenario
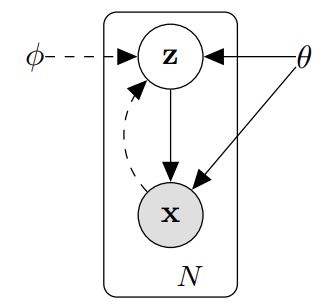
$X$ : 연속적인 혹은 이산적인 변수 $x$ N개의 i.i.d sample을 포함하는 데이터 셋
$z$ : 관측되지 않은 연속형 랜덤 변수
$x$ : z를 포함하는 어떤 random process에 의해 생성 (사전 분포 $p(z)$로부터 생성)
(1) Intractability : Marginal Likelihood를 직접 구하기 어렵다.
(2) A large dataset : 데이터가 많아 Batch Optimization에서 비용이 많이 든다.

이에 대한 3가지 해결책
(1) 파라미터 $\theta$에 대한 효과적인 근사치인 ML 또는 MAP 추정
(2) 관측 값 $x$가 주어졌을 때 잠재 변수 $z$의 효과적인 근사치 추정
(3) x의 효율적인 Approximate Marginal Inference
이 상황에서 우리가 찾고자 하는 $p_{\theta}(x)$를 직접 알아내는 것은 어렵다. 따라서 컨트롤 할 수 있는 Latent Variable z를 활용하여 $p_{\theta}(x)$에 간접적으로 접근한다.
$$ p_{\theta}(x) = \int p_{\theta}(x,z) dz = \int p_{\theta}(z)p_{\theta}(x|z)dz $$
$p_{\theta}(z)$ : Prior, 풀고자 하는 문제에 대한 우리의 가정으로 z가 특정 확률 분포를 따를 것이라는 가정을 말한다. 주로 Gaussian 정규 분포로 가정을 진행하며, 이 때 Log를 취하는 것은 데이터를 모델에 넣을 때 불안정한 값을 변환해 주는 것
$p_{\theta}(x|z)$ : Likelihood, 우리가 만들고자 하는 생성 모델(컨트롤 할 수 있는 z에 의해 데이터가 만들어지기 때문)
Prior $p_{\theta}(z)$는 컨트롤 가능한 확률분포로 설정할 때 편리하기 때문에 VAE 모델은 이를 정규분포로 설정하였고, 이제 Prior를 정하는 문제는 정규분포의 $\mu$와 $\sigma$를 구하는 문제로 변하게 된다.
2.2. The variational bound
이전까지는 Intractable한 $p_\theta$를 알아내기 위해 Variational Inference를 사용하였다. Variational Inference는 구하기 어려운 사후 확률 분포를 우리가 알고 있는 확률 분포로 근사하는 것을 의미한다. 여기서 Variational Inference는 알고 있는 확률 분포와 사후 확률 분포의 차이를 줄이는 방향으로 학습되며, KL Divergence를 이용해 계산한다.
https://hyeongminlee.github.io/post/bnn003_vi/
Variational Inference | Hyeongmin Lee's Website
앞선 포스팅에서 우리는 MLE와 MAP에 대하여 알아봤습니다. MLE는 Likelihood만 주어진 경우 이를 최대로 하는 parameter를 찾는 일이고 MAP는 Likelihood와 사전 지식인 Prior가 전부 주어진 경우 Posterior를 최
hyeongminlee.github.io
$$ \begin{align} \log p_{\theta}(x) &= \mathbb{E}_{z \sim q_{\phi}(z|x)} [ \log p_{\theta}(x) ] \\ &= \mathbb{E}_{z \sim q_{\phi}(z|x)} \left[ \log \left[\frac{p_{\theta}(x,z)}{p_{\theta}(z|x)} \right] \right] \\ &= \mathbb{E}_{z \sim q_{\phi}(z|x)} \left[ \log \left[\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)} \frac{q_{\phi}(z|x)}{p_{\theta}(z|x)} \right] \right] \\ &= \mathbb{E}_{z \sim q_{\phi}(z|x)} \left[ \log \left[\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)} \right] \right] + \mathbb{E}_{z \sim q_{\phi}(z|x)} \left[ \log \left[\frac{q_{\phi}(z|x)}{p_{\theta}(z|x)} \right] \right] \\ &= \mathcal{L}_{\theta, \phi}(x) + D_{\textrm{KL}}(q_{\phi}(z|x)||p_{\theta}(z|x)) \end{align} $$
- z를 랜덤하게 뽑아 만들어 낸 $logp_{\theta}(x)$의 기대값은 최대가 되어야 한다.
- 위 식에서 $\mathcal{L}_{\theta, \phi}(x)$를 ELBO(Evidence Lower BOund)라고 한다.
- $D_{\textrm{KL}}$은 거리 개념이기 때문에 항상 0보다 크다. KL Divergence는 작을 수록 좋기 때문에, ELBO를 최대로 만드는 것이 $logp_{\theta}(x)$를 최대로 만드는 것이 된다.
- 식을 넘겨 ELBO에 관한 식으로 만들게 되면 아래와 같은 식이 된다.
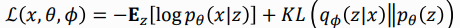
$\mathbb{E}_{z \sim q_{\phi}(z|x)} \left[ \log p_{\theta}(x|z) \right]$ 최대화
이 항은 latent variable로 복구된 결과 $x$에 대한 기대값으로, 다른 말로 reconstruction term이라 한다. ELBO가 최대화되려면 reconstruction term으로 복구된 결과의 기대값이 높아야 한다.
reconstruction term은 Expectation 형태로 되어있기 때문에 적분 형태로 바꿔줄 수 있지만, z에 대한 적분은 계산하기 쉽지 않다. 따라서 이때 Monte-Carlo Technic을 사용한다. 어떤 분포를 가정하고 그 분포에서 무한개 혹은 굉장히 큰 수의 sampling을 해서 평균을 내면 그것이 실제 true 기댓값과 거의 동일해질 것이라는 가정이다.
$- D_{\textrm{KL}}(q_{\phi}(z|x) || \log p_{\theta}(z))$ 최대화
이 항은 인코더 네트워크가 만들어낸 latent variable $z$의 확률분포와 우리가 원했던 latent variable $z$의 확률분포 사이의 연관성을 설명한다. 당연히 그 연관성이 높아야 하므로 $D_{\textrm{KL}}$은 최소로 되어야 하고, $-D_{\textrm{KL}}$는 최대화 되어야 할 것이다. 이 항을 다른 말로 regularization term이라 한다.
※ Regularization의 효과
1. Continuity
: 비슷한 성질을 가진 데이터들이 비슷한 위치의 Latent Space에 매핑되어 가까이 위치한 z에서 만들어지는 Sample끼리 서로 비슷하기를 기대
2. Completeness
: Latent Space에서 Sampling되어지는 z는 유의미한 정보를 포함하고 있어야 함
2.3. The SGVB estimator and AEVB algorithm
- 최적화 하고 싶은 Lower Bound와 미분 값에 Estimator를 적용
- Gradient Based Optimization이 가능

2.4. The reparameterization trick
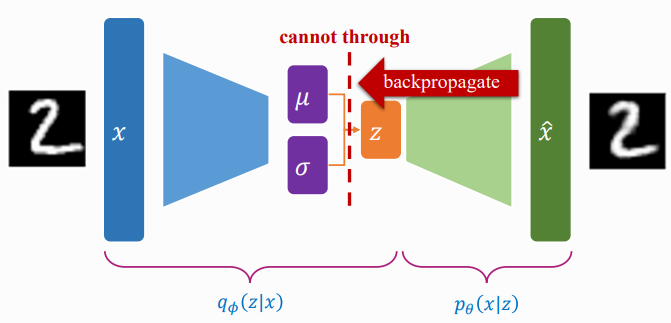
z를 직접 Sampling 할 경우 Random 연산은 미분이 불가능하기 때문에 역전파가 불가능하다. 따라서 Reparameterization trick을 사용하는데, 이는 z를 $N(\mu, \sigma)$에서 직접적으로 Sampling하지 않고 Deterministic output vector + Gaussian Noise로 계산하는 것이다.
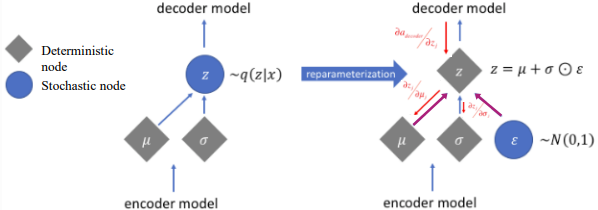
이 때 새로운 vector인 $\epsilon$을 이용해서 새로운 확률 변수를 계산한다. 예를들어 $\mu$와 $\sigma$를 알 때 $\mu + \sigma*\epsilon$과 같이 확률 변수를 사용하는 것이다.
논문에서는 몇가지 Reparametrization Function에 대한 팁을 제공한다.
(1) Inverse CDF로 정의한 뒤, $\epsilon$을 Uniform(0,1) 균등 분포에서 Sampling하여 계산
(2) Gaussian과 유사한 경우 Location-scale을 설정하여 Location + scale*epsilon으로 정하고, epsilon을 정규분포(0,1)에서 sampling하여 계산
(3) 다른 보조 변수들의 변환으로 계산
VAE에서는 Likelihood를 NeuralNet으로 모델링하고 그 출력은 영상이 된다.
NeuralNet을 recognition 모델로 쓸 경우, 본 논문에서 제안하는 내용이 variational auto-encoder가 되고, Variational approximate posterior를 다음과 같이 multivariate Gaussian으로 잡는다.
$$\log q_{\phi} (z | x^{(i)}) = \log\mathcal{N}(z; \mu^{(i)}, \sigma^{2(i)}\mathbf{I})$$
이제 다음의 ELBO 수식의
$$\mathcal{L}(\theta, \phi, x^{(i)}) \simeq -D_{\mathrm{KL}}(q_{\phi}(z|x^{(i)}) || p_{\theta}(z)) + \mathbb{E}_{q_{\phi}(z|x^{(i)})}[\log p_{\theta}(x^{(i)}|z)]$$
우항 첫번째 term은 다음과 같이 쓸 수 있다.
$$ -D_{\mathrm{KL}}(q_{\phi}(z|x^{(i)}) || p_{\theta}(z)) = \frac{1}{2} \sum_{j=1}^{J} \left( 1 + \log((\sigma_{j}^{(i)})^2)) - (\mu_j^{(i)})^2 - (\sigma_j^{(i)})^2 \right) $$
여기서 $J$는 latent space의 dimension을 나타낸다. 우항 두번째 term은 Monte Carlo estimation으로 다음과 같이 쓸 수 있다.
$$\mathbb{E}_{q_{\phi}(z|x^{(i)})}[\log p_{\theta}(x^{(i)}|z)] = \frac{1}{L}\sum_{l=1}^{L} \log p_{\theta}(x^{(i)}|z^{(i,l)})$$
여기서 $L$은 몬테카를로 샘플 개수를 나타낸다. 따라서, ELBO 수식은 다음과 같이 근사될 수 있다.
$$\mathcal{L}(\theta, \phi, x^{(i)}) \simeq \frac{1}{2} \sum_{j=1}^{J} \left( 1 + \log((\sigma_{j}^{(i)})^2)) - (\mu_j^{(i)})^2 - (\sigma_j^{(i)})^2 \right) + \frac{1}{L}\sum_{l=1}^{L} \log p_{\theta}(x^{(i)}|z^{(i,l)})$$
3. Example: Variational Auto-Encoder
이 파트에서는 Probabilistic encoder에 NeuralNet을 사용하여 AEVM 알고리즘에서 파라미터를 최적화 시키는 예시를 보여준다.
Prior를 Multivariate Gaussian으로 가정할 경우 True Posterior는 Interactiable하기 때문에 Posterior를 Multivariate Gaussian으로 Approximation한다.
<참고자료>
https://medium.com/humanscape-tech/paper-review-vae-ac918509a9ba
[Paper Review] VAE
Variation AutoEncoder 살펴보기
medium.com
https://dongju923.github.io/paper/VAE
VAE 논문리뷰
원문링크: Auto-Encoding Variational Bayes
dongju923.github.io
https://di-bigdata-study.tistory.com/5
[VAE] Auto-Encoding Variational Bayes 논문 정리(2)
VAE의 두번째 글이다. 앞의 글에서는 VAE의 기본구조와 VAE를 학습하기 위해서 input data x의 likelihood를 최대화하는 수식들을 따라가며 ELBO를 도출하는 것까지 살펴보았다. 이제부터는 ELBO를 이용해
di-bigdata-study.tistory.com
국민대학교 김준호 교수님 VAE 강의자료
국민대학교 박종혁 교수님 VAE 강의자료
여러 줄 요약
1. 기존 이미지와 가장 비슷하게 이미지를 생성해 주는 함수 $p_{\theta}(x)$를 구하고 싶음
2. 하지만, $p_{\theta}(x)$는 직접 구하기 힘들기 때문에 컨트롤 가능한 z를 추가하여 $p_{\theta}(x, z)$문제로 변경
3. 이 때 학습 과정에서 만들어지는 z는 내가 알고있는 p(z)와 비슷하게 만들고 싶음 -> KL Divergence 사용
4. 이 때 MLE, MAP 방식을 사용할 수 없고 MCMC 방식은 계산량이 많기 때문에 AEVB 방식을 사용 (Variational Inference)
5. 수식 유도 과정을 살펴보면 ELBO를 최대화하는 것이 $p_{\theta}(x)$를 최대화 하는 것을 알 수 있음 (이 때 Log 사용)

'논문 paper 리뷰' 카테고리의 다른 글
| [X:AI] StarGAN 논문 이해하기 (0) | 2023.05.25 |
|---|---|
| [Paper Review] GLocal-K 논문 이해하기 (0) | 2023.04.27 |
| [X:AI] SegNet 논문 이해하기 (0) | 2023.04.19 |




댓글