대부분 Attention을 처음 접하게 되는 것은 Transformer 모델을 공부하면서부터일 것이다. 나 또한 그랬으며 처음 Transformer 모델을 공부한 후 Attention이라는 단어는 수없이 들었던 것 같다. 하지만, 나는 Attention을 잘 모른다. 정확히 말하면 알았지만 까먹었다가 또 공부하고 또 까먹는 악순환을 반복하는 중이다...
볼 때는 기억나지만 안보면 또 까먹게 되는 마성의 Attention! 이번 기회에 틈틈히 볼 수 있도록 꼼꼼히 정리해보려 한다.
Attention은 말 그대로 알고자하는 내용과 관련된 부분을 집중(Attention)하여 모델의 성능을 올리는 기법이다.
기본적인 아이디어는 "전체 벡터를 동일한 비율로 참고하는 것이 아니라, 알고자하는 시점의 벡터와 관련있는 벡터를 더 집중(Attention)해서 보자"이며, 여기서는 조금 더 디테일한 이해를 돕기 위해 벡터라는 워딩을 사용하였다(NLP의 경우 단어, CV의 경우 픽셀(패치)이라고 생각해도 좋다).

Attention 함수를 이루는 Query, Key, Value 중 Key, Value는 파이썬의 기본 자료형인 딕셔너리의 Key, Value와 비슷한 역할을 수행한다. 즉, 특정 Key에 대응되는 Value를 가지고 있다고 볼 수 있으며 Attention 함수는 다음과 같이 표현할 수 있다.
$$Attention(Query, Key, Value) = Attention Value$$
Attention 함수는 주어진 Query를 가지고 모든 Key에 대한 유사도를 계산하고, 구한 유사도를 키에 매핑되어있는 각각의 Value에 반영한다. 이 때 반영된 Value 들을 모두 더한 값을 Attention Value라고 한다.
NLP Task 속 Query, Key, Value의 의미
- Query : t시점의 디코더 셀에서의 Hidden State
- Key : 모든 시점 인코더 셀의 Hidden States
- Value : 모든 시점 인코더 셀의 Hidden States
Attention에는 다양한 종류가 있지만, 그 중 대표적이고 간단히 표현할 수 있는 Dot-Product Attention에 대해 설명하도록 하겠다.
Dot-Product Attention

위 그림은 Decoder의 3번째에 위치한 LSTM 셀에서 출력 단어를 예측할 때 Attention을 사용하는 예시 그림이다. Decoder의 3번째 LSTM 셀은 출력 단어를 예측하기 위해 Encoder의 모든 입력 단어들의 정보를 참고한다. 이 때 Encoder 셀 각각의 Output 결과에 Softmax를 함수를 사용하여 Encoder 각각의 단어가 Decoder에서 현재 시점의 단어를 예측하는데 얼마나 도움이 되는지를 측정한다(유사도 계산).
이후 해당 정보를 담아 Decoder에 보낸 후 출력 단어를 예측하는데 활용한다.
Attention을 수행하는 과정을 간단하게 설명하면 위와 같은데, 이를 자세히 풀어 설명해보도록 하겠다.
1. Attention Score 구하기

위 그림에서 $h_1$, $h_2$, $h_3$, $h_4$는 Encoder의 hidden state(Key, Value)이고 $s_t$는 현재 시점 Decoder 셀의 hidden state(Query)이다. 이 때 Encoder와 Decoder의 hidden state 차원이 같다는 가정이 수반되며 위 그림에서 차원은 4로 표현되어 있다.
현재 시점 t에서의 출력 단어를 예측하기 위해서 들어가는 Input은 t-1시점의 hidden state와 t-1시점의 출력 단어이다(일반적인 RNN 구조). Attention 매커니즘은 여기에 더하여 Attention Value를 함께 사용해 주는데 그러기 위해서는 우선 Attention Score를 구해주어야 한다.
여기서 Attention Score란 Encoder의 모든 Hidden state들이 각각 Decoder의 t시점 hidden state $s_t$와 얼마나 유사한지 판단하는 Score 값이다.
이 때 유사도를 구하는 방법에 따라 다양한 Attention 매커니즘이 존재하며 여기서는 Dot-Product를 통해 Attention Score를 구해준다. Dot-Product는 일반적으로 알고있는 내적으로 Vector끼리의 연산을 수행하는 것을 의미하며 그 식은 아래와 같다.
$$ score(s_t, h_i) = s_t^Th_i$$
그렇게 계산한 Attention Score들은 다음과 같이 표현할 수 있다.
$$AttentionScore_t = [s_t^Th_1, s_t^Th_2, s_t^Th_3, s_t^Th_4]$$
2. Softmax 함수를 통해 Attention Distribution 구하기

앞서 계산한 t시점의 AttentionScore에 Softmax 함수를 적용하면 모든 값을 합할 때 1이 되는 확률 분포를 얻을 수 있다. 이를 Attention Distribution이라고 부르며, 각각의 값을 Attention Weight라고 부른다.
예를 들어 위 그림에서 I, am, a, student에 대한 Attention Score $s_t^T h_1, s_t^T h_2, s_t^T h_3, s_t^T h_4$에 Softmax를 취한 Attention Weight가 각각 0.1, 0.4, 0.1, 0.4(합이 1)라고 할때, 이에 해당하는 Attention Distrubution의 시각화된 크기가 Attention Weight가 클 수록 큰 것을 알 수 있다.
3. Encoder의 각 Attention Weight와 Hidden State를 가중합하여 Attention Value 구하기
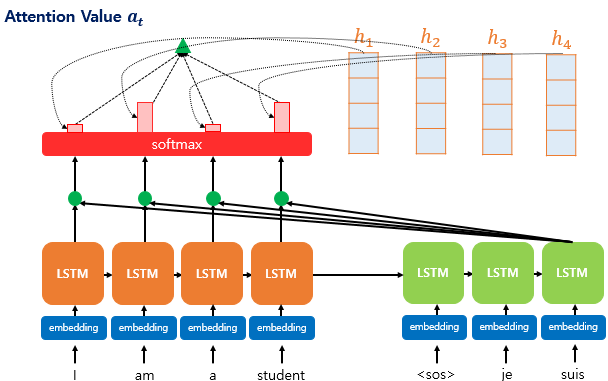
기존에 존재했던 Encoder의 각 Hidden State(Value로 볼 수 있음)에 Attention Weight를 가중합해준다. 예를 들어 4차원인 $h_1$에 Attention Weight의 첫번째 값을 동일하게 모두 곱해준 후 나온 값 전부를 더해준다.
이렇게 되면 Encoder의 단어 수만큼(I, am, a, student)의 값이 나오며 이를 Attention Value(Convtex Vector)라고 한다. 이 때 Encoder의 Context를 포함하고 있다고 하여 Context Vector라고도 부른다.
이렇게 얻은 Attention Value를 $a_t$로 표현
4. Attention Value와 Decoder의 t시점 hidden state 연결
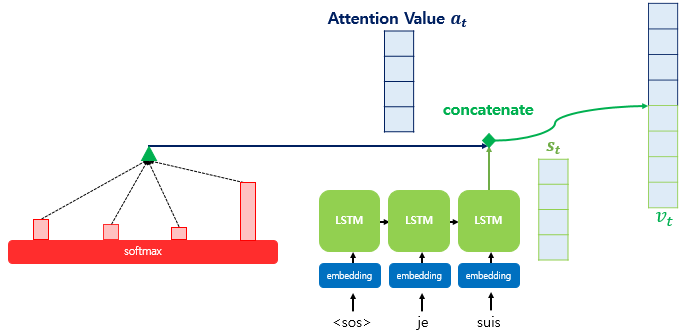
3단계까지의 과정을 거쳐 Attention Value를 구했다면 이제 다시 t시점의 hidden state인 $s_t$와 결합(Concatenate)하는 과정을 거쳐야 한다. 이 두가지 정보가 합쳐져(Encoder에서 얻은 정보를 활용하여) $\hat{y}$를 더 잘 예측하게 된다.
Attention Value $a_t$와 $s_t$가 결합된 Vector를 $v_t$로 표현
5. Output Layer 연산의 Input이 되는 $s_t$를 계산
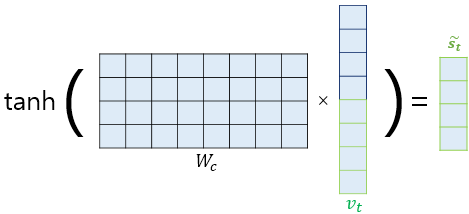
논문에서는 4단계까지의 과정을 거쳐 만들어진 Attention Value $v_t$를 바로 사용하지 않고 신경망 연산을 한 번 더 거쳤다. 가중치 행렬과 tanh 함수를 거쳐 Output Layer의 Input이 되는 $s_t$를 만들었고 이를 사용하여 아래와 같은 형태로 예측 벡터를 얻게 된다.$$\hat{y}_t = Softmax(W_y\tilde{s}_t + b_y)$$
다양한 종류의 Attention

중간의 유사도를 계산하는 수식의 차이에 따라 위와 같이 여러 종류의 Attention 기법이 존재한다.
참고자료
15-01 어텐션 메커니즘 (Attention Mechanism)
앞서 배운 seq2seq 모델은 **인코더**에서 입력 시퀀스를 컨텍스트 벡터라는 하나의 고정된 크기의 벡터 표현으로 압축하고, **디코더**는 이 컨텍스트 벡터를 통해서 출력 …
wikidocs.net
작성한 글은 제가 공부해온 내용을 바탕으로 추론한 개인적인 생각이 들어가 있습니다. 잘못 된 점이 있다면 언제든 수정하여 알려주시면 감사하겠습니다.
'AI & CS 지식 > 인공지능 Q&A' 카테고리의 다른 글
| [AI Q&A] OKS(Object Keypoint Similarity)란? (1) | 2024.11.22 |
|---|---|
| [AI Q&A] Inductive Bias란 무엇일까? (1) | 2024.08.13 |
| [AI Q&A] GAN 모델이 가지는 문제점은 무엇일까? (0) | 2024.08.12 |




댓글