[Paper Review] Unbiased Data Processing for Human Pose Estimation 논문 이해하기
『 The Devil is in the Details: Delving into Unbiased Data Processing for Human Pose Estimation. CVPR. 2020. 』
지금까지는 주로 성능을 높이기 위해 여러 기법들을 결합한 Pose Estimation 모델들에 대해 알아보았다. 이 모델들은 대부분 Object Detection이나 Segmentation과 같이 다른 Computer Vision Task에서 좋은 성능을 냈던 기법들을 가져와 Pose Estimation Task에 녹이는 방법을 사용하였는데, 이번에 소개할 논문에서는 Human Pose Estimation에서 성능을 높이려면 어떻게 해야할지를 먼저 고민하였다.
Devil is in the Details 라는 문구는 영어 관용어로 문제점이나 불가사의한 요소가 세부사항 속에 숨어있다는 의미이다. 그만큼 지금까지의 Human Pose Estimation에서 일반적으로 사용하던 방법 속에 문제가 있다는 점을 저자들이 지적하고 싶었던 것이라고 생각한다. 그럼 이제 논문의 핵심 내용을 한 번 알아보도록 하자 :)
본래 20년도 CVPR에 제출된 논문이 아닌 아카이빙 버전의 후속 논문을 읽고 리뷰를 진행하였다(HigherHRNet과의 결합이 얼마나 잘 되었는지를 확인하기 위해...).
Github
https://github.com/HuangJunJie2017/UDP-Pose?tab=readme-ov-file
GitHub - HuangJunJie2017/UDP-Pose: Official code of The Devil is in the Details: Delving into Unbiased Data Processing for Human
Official code of The Devil is in the Details: Delving into Unbiased Data Processing for Human Pose Estimation - HuangJunJie2017/UDP-Pose
github.com
0. Abstract
본 논문은 학습과 추론 과정에서 중요한 문제이지만 Human Pose Estimation에서는 아직 체계적으로 고려되지 않은 Data Processing에 대해 다룬다. 연구를 통해 Human Pose Estimation의 주요 문제 중 하나가 편향된 Data Processing인 것을 발견하였으며, 지금까지 일반적으로 사용해오던 Flipping 전략에 문제가 있다는 점과 일부 Keypoint Format Transformation 방법에 통계적 오류가 있다는 점을 알아내었다.
따라서 본 논문에서는 이러한 2가지 문제를 해결하기 위해 각 문제에 대응하는 2가지 기술로 구성된 UDP(Unbiased Data Processing) 기법을 제안한다. UDP를 기반으로 기존 편향된 Data Processing의 문제를 제거하고 차선책들을 연구하였으며 기존 모델들에 UDP 기법을 결합하여 SOTA를 기록하였다.
즉, 이전에 사용한 Coordinate System Transformation(Flipping 전략)과 Keypoint Format Transformation에 문제가 있어서 각각의 문제를 해결할 수 있는 기술 2가지를 결합한 UDP 기법을 제안
1. Introduction

Human Pose Estimation의 Metric은 실제 값과 예측 결과간의 위치 Offset을 기반으로 계산되기 때문에 다른 컴퓨터 비전 Task에 비해 Data Processing에 더 민감하게 반응한다. 하지만 이러한 중요성에도 불구하고 Human Pose Estimation에서는 아직 Data Processing에 대한 체계적인 연구가 진행되지 않았다.
본 논문에서는 기존 Human Pose Estimation에서 진행한 Data Processing의 문제점을 발견하였는데 이는 아래의 2가지이다.
- Flipping(좌우 반전) 전략을 사용 할 때 반전된 이미지에서 얻은 결과가 원본 이미지의 결과와 일치하지 않는다.
- 결함있는 Keypoint Format Transformation 방법이 Precision을 떨어뜨린다.
여기서 말한 Keypoint Format Transformation 방법이 무엇일까? 논문을 읽으며 해당 부분을 찾아보자. 참고로 HigherHRNet에서는 이러한 Keypoint Format Transformation 문제를 Network 출력 해상도를 높임으로써 해결했지만 대신 Latency가 많이 늘어났다고 한다.
본 논문에서는 이러한 2가지 문제를 해결하기 위한 UDP(Unbiased Data Processing) 시스템을 제안한다. UDP는 위의 문제에 대해 각각 Unbiased Coordinate System Transformation과 Unbiased Keypoint Format Transformation이라는 방법으로 대응한다.
Unbiased Coordinate System Transformation을 목표로 Continuous Space에서 이 문제를 정의하고 분석하는 원칙을 만들고 이 원칙을 바탕으로 다양한 기본 변환들(cropping, resizing 등)에서의 Coordination System Transformation을 설계한다. Unbiased Keypoint Format Transformation으로는 2가지 방법을 소개하였으며 전형적인 biased 방법들에 대한 분석을 진행하였다.
UDP 방법을 통해 앞에서 말한 2가지 문제를 해결할 수 있었고 COCO와 CrowdPose 데이터 셋을 활용한 여러 실험을 통해 UDP의 좋은 성능을 확인할 수 있었다.
2. Related Work
지금까지의 Bottom-Up과 Top-Down, 그리고 Pose Estimation에서의 Data Processing에 대해 서술하고 있다. Top-Down이나 Bottom-Up 모델들에 대한 내용은 많이 공부해 보았으니 넘어가고(논문 참고) Data Processing에 집중해 보도록 하겠다.
Human Pose Estimation에서의 Data Processing은 주로 Coordinate System Transformation과 Keypoint Format Transformation으로 나타난다. Coordinate System Transformation은 Cropping, Resizing, Rotating같은 작업을 수행하며 데이터(Keypoint나 이미지 Matrix)를 다른 Coordinate로 바꾸는 것을 의미한다. CPN, SimpleBaseline, HRNet 등 최신 모델들은 이미지 크기를 조정할 때 픽셀을 사용하는데 이 때 Flipping을 사용할 경우 결과가 맞지 않고 bias가 발생한다. 이런 오류를 억제하기 위해 기존 모델들은 Flipping된 이미지 결과를 1 픽셀 움직이거나(SimpleBaseline, HRNet, Darkpose) 좌표계 평균을 2 픽셀 움직이기도 하였다(CPN, MSPN).
👉 Unbiased Coordinate System Transformation 제안
Keypoint Format Transformation은 일반적으로 관절 좌표나 Heatmap 간의 변환을 의미한다. 학습 과정에서는 Annotation된 Keypoint 좌표를 Gaussian 분포를 가진 Heatmap으로 인코딩하고, 테스트 과정에서는 네트워크가 예측한 Heatmap을 다시 Keypoint로 디코딩한다. 이러한 파이프라인은 Keypoint를 직접 Regression하는 것보다 성능이 좋지만 완벽하지는 않다.
👉 Keypoint Format Transformation이란 기존 Heatmap 기반의 예측 방식을 의미하는 것이었구나!
3. Unbiased Data Processing for Human Pose Estimtaion
3.1. Unbiased Coordinate System Transformation
Unbiased Coordinate System Transformation을 위해 본 논문에서는 Continuous Space에서 데이터에 대한 통일된 정의를 만들고, 이 정의를 기반으로 Coordinate System Transformation의 개념과 편향되지 않은 Coordinate를 만드려는 목적을 소개한다.
계속해서 언급되는 Coordinates는 각 Layer마다의 Feature를 의미한다. Source Image, Network Input, Network Output 각각을 하나의 Coordinates라고 말하고 있다.
Coordinates 간의 변환을 구성하기 전 기본 단계(Resizing, Cropping 등)에서 설계를 진행하며 수학적 논리를 통해 Coordinate 변환 Pipeline의 Unbias를 검증한다. 또한 Bias Data Processing에 대한 연구도 진행하였다.
3.1.1. An Unified Definition of Data in Continuous Space
논문을 여기까지 읽었을 때 가장 이해가 안된 부분이었다. Continuous Space에서 어떤 정의를 한다는 것인지?

이미지 Matrix는 Discrete Format에서 처리되지만 Keypoint Coordinate는 Continuous Space에서 처리된다.
이미지는 RGB로써 정수 좌표를 가지지만 Keypoint는 소수점 단위로 표현할 수 있기 때문에 Continuous Space에 존재한다.
따라서 Coordinate를 변환하는 과정에서 Precision이 낮아지지 않도록 서로 다른 데이터를 일관되게 분석하고 처리할 수 있는 통일된 패러다임이 필요하다. 본 논문에서는 이를 위해 연속적인 이미지 평면이 존재한다고 가정하고 각 이미지 Matrix를 해당 평면에서 Discrete Sampling한 결과로 간주한다. Image Matrix의 각 Pixel은 특정 샘플링 지점을 의미한다.
이미지 Matrix정보가 R, G, B 3차원인 x, y 좌표 상의 정수값으로 표현된 것이 사실은 3차원인 Float Matrix에서 Discrete Sampling을 해서 얻은 정보라고 말하고 있는 것이다.
수식으로 표현하면 다음과 같다.
$$\textbf{I}(p) = (r, g, b) | p = (x, y), x \in \{0, 1, 2 ... w\}, y \in \{0, 1, 2, ...h\}$$
$$k = (x, y)$$
- $\textbf{I}$ : Image Plane
- $k$ : target keypoint
- $w^p$ : 픽셀로 계산된 Image Matrix의 Width
- $h^p$ : 픽셀로 계산된 Image Matrix의 Height
- $w = w^p - 1$
- $h = h^p - 1$
- 본 논문에서 말하는 $w, h$는 일반적으로 사용하는 해상도 단위가 아니다.
👉 Continuous Space 데이터에 대한 통일된 정의 : Image 데이터가 연속적인 Image Plane에서 샘플링 된 결과라는 가정
3.1.2. The Concept of Coordinate System Transformation
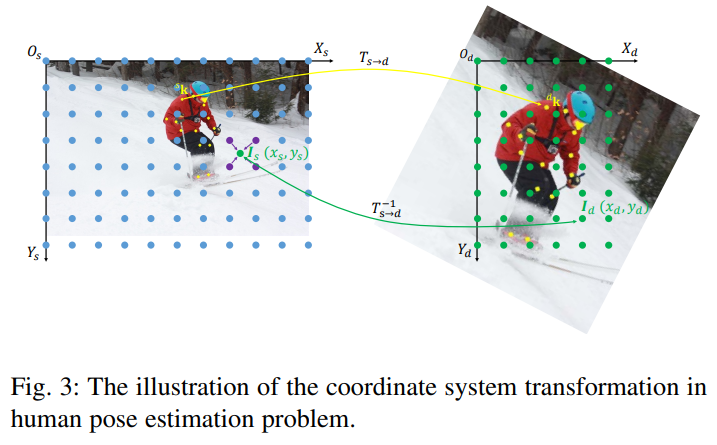
Figure 3에서 나타난 $O_s$, $X_s$, $Y_s$는 Source Coordinate를, $O_d$, $X_d$, $Y_d$는 Destination Coordinate를 나타낸다. 이 때 $s$ Coordinate Keypoint에서 $d$ Coordinate Keypoint로의 변환은 아래와 같이 표현할 수 있다.
$$k_d = T_{s \rightarrow d}k_s$$
그리고 Image Matrix상의 내용을 변환하는 식은 다음과 같다. 이 때 중요한 것은 Image 속 내용이 Source Coordinate와 Destination Coordinate에서 동일한 의미를 가지도록 변환해야 한다는 것이다.
$$\textbf{i}_d(p_d) = \textbf{i}_s(T^{-1}_{s\rightarrow d}p_d)$$
$p$는 해당 Coordinate에서의 특정 위치를 말하며 이 때 두 Coordinate에서 동일한 의미를 갖기 위해 $p_d$의 색상 정보를 Source 이미지의 대응 위치 $T^{-1}_{s \rightarrow d}p_d$에서 가져온다. 이러한 과정을 백트래킹(Backtracking)이라고 한다.
물론 이렇게 구한 값은 대개 정수가 아니라 소수점으로 나오기 때문에 이산적인 픽셀 값과 일치하지 않는다. 따라서 Bilinear Interpolation을 사용하여 주변 값들을 계산에 활용한다(보간법을 많이 사용하면 정밀도가 떨어지기 때문에 적게 사용하는 것이 좋음).
3.1.3. The Targets of Unbias
Unbiased Coordinate 변환의 목표는 두 가지이다.
- 의미적인 정렬(Semantical Alignment) 유지
- 예측 결과와 실제 값의 정확한 정렬(Alignment)
우선 첫번째에서 말하는 의미적인 정렬이란 데이터 간의 상대적인 위치 관계가 변환 후에도 유지되는 것을 말한다. 따라서 변환 행렬을 일관되게 유지하는 것이 중요하다.
두번째 목표는 예측 결과가 실제 값(Ground Truth)와 일치하도록 만드는 것이다. 결국 좌표 변환 후에도 데이터의 의미가 잘 보존되며 정밀도가 떨어지지 않도록 만드는 것이 Unbiased Coordinate Transformation의 목적이다.
3.1.4. Coordinate System Transformation in Elementary Operations
Human Pose Estimation에서 자주 사용하는 기본적인 4가지 연산(Cropping, Resizing, Rotating, Flipping)에 대해 소개하고 있다.
Cropping
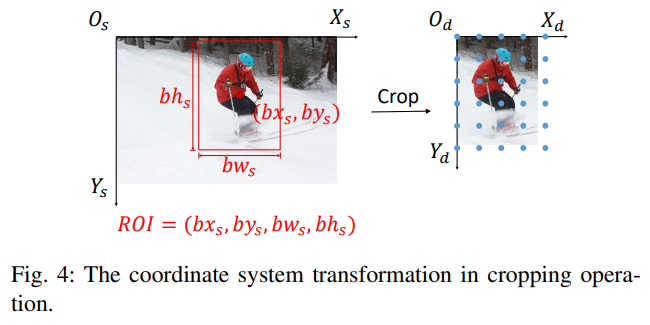
Cropping은 특정 ROI(Region of Interest)를 기준으로 이미지를 잘라내는 방법이다. Destination Coordinate에서는 잘라낸 ROI의 좌측 상단 모서리를 원점으로 이동시킨다.
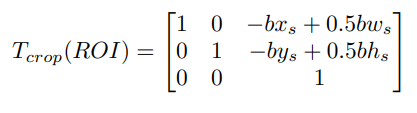
Resizing
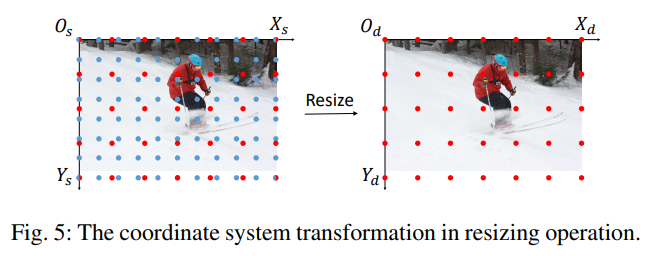
Resizing의 경우 의미적인 내용은 동일하게 유지하면서 Sampling 전략을 바꾸는 방법이다. Source Coordinate와 Destination Coordinate의 네 모서리 샘플 포인트가 의미적으로 정렬하도록 만든다.

- $w_s$, $h_s$ : Source Image width, height
- $w_d$, $h_d$ : Destination Image width, height
Rotate
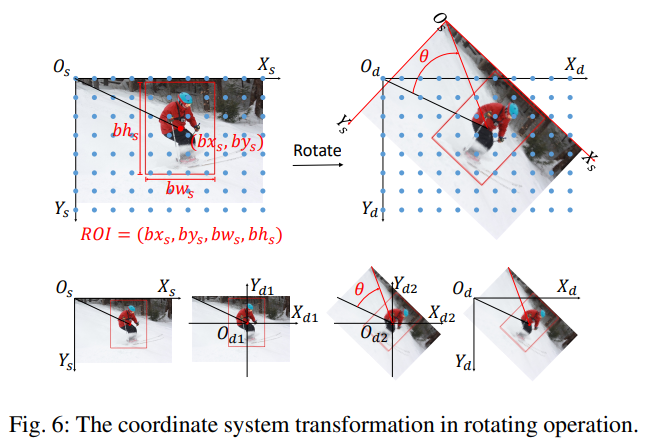
Rotate는 특정 ROI를 기준으로 수행되며 좌표계의 중심 대신 ROI의 중심이 회전 중심이 된다. 이 때 ROI는 Top-Down 방식에서는 Bounding Box를, Bottom-Up 방식에서는 전체 이미지를 의미한다. 회전 변환은 3가지 기본 변환의 조합으로 이루어지며 이를 결합하면 아래와 같다.
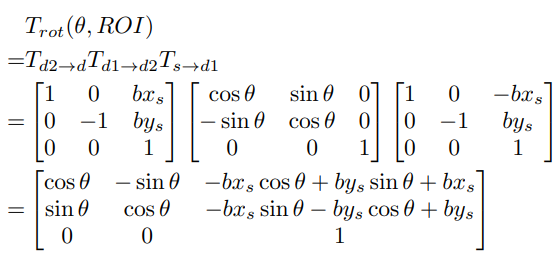
Flipping
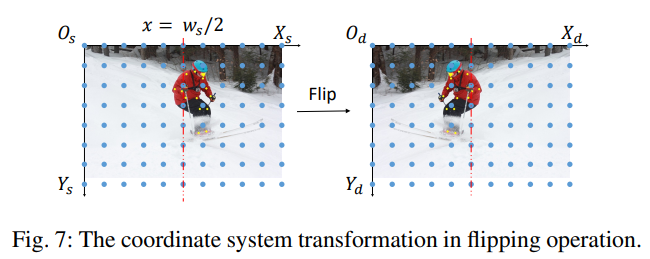
Flipping은 일반적으로 Source Image 너비의 중간을 기준으로 좌우로 반전시키는 방법이다.
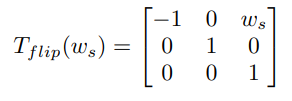
👉 수식을 가지고 어렵게 설명했지만 일반적으로 알고 있는 4가지 Transformation 방법을 소개
3.1.5. Common Coordinate System Transformation
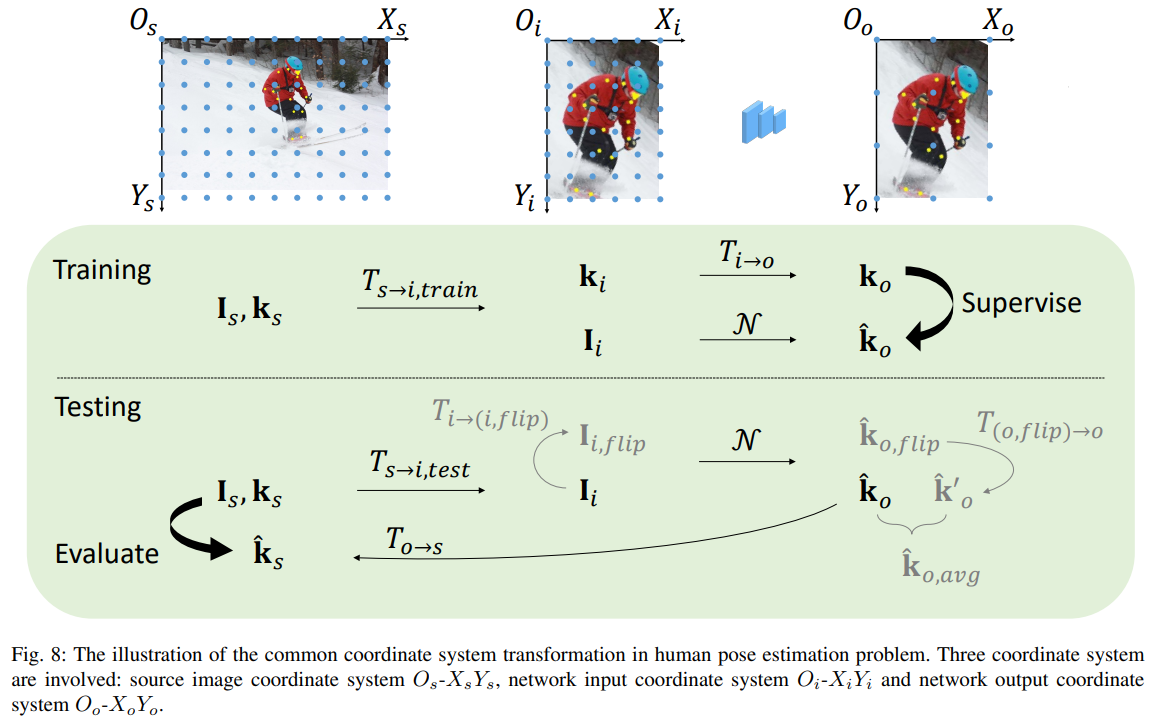
$i$와 $o$는 각각 네트워크의 입력 좌표계, 네트워크의 출력 좌표계를 의미한다.이러한 좌표계들은 변환 과정에서 중요한 역할을 하기 때문에 편향되지 않고 정확하게 수행되도록 설계되어야 한다.
Training 과정 속 변환
1. $O_s$ -> $O_i$ 이 때 4가지 기본 변환이 사용됨 $T_{s\rightarrow i, train}$
2. 변환된 이미지 행렬 $I_i(p_i)$가 네트워크 입력으로 사용되며 출력으로는 예측된 Keypoint $\hat{k}_o$를 생성
3. Ground Truth Keypoint는 네트워크 입력 Coordinate에서 출력 Coordinate로 변환된 후($k_o$) 예측된 Keypoint 와의 차이를 최소화 하는데에 사용됨
Test 과정 속 변환
1. Test 시에는 Training 과정처럼 원본 이미지에 기본 변환이 적용되지만 필수적인 Cropping과 Resizing만 적용되고 Rotating이나 Flipping은 사용되지 않는다. $T_{s\rightarrow i, test}$
2. 네트워크를 통과해 나온 $\hat{k}_o$는 역변환을 통해 Source Coordinate로 변환되어 최종 예측 Keypoint $\hat{k}_s$가 된다.
다음의 식 16은 Source Coordinate에서 예측한 Keypoint가 실제 Keypoint와 정확히 일치하는 것을 보여준다. 이는 Transformation Pipeline이 Biased 하지 않다는 것을 의미한다.
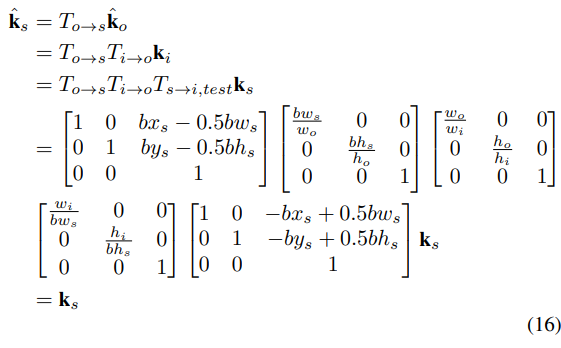
기존 Transformation에서는 Flipping을 사용하였을 데 문제가 있었지만, 본 논문의 Transformation 방법을 따르면 식 19와 같이 Flipping을 하더라도 원본 이미지와 동일한 예측 결과가 나오는 것을 확인할 수 있다.
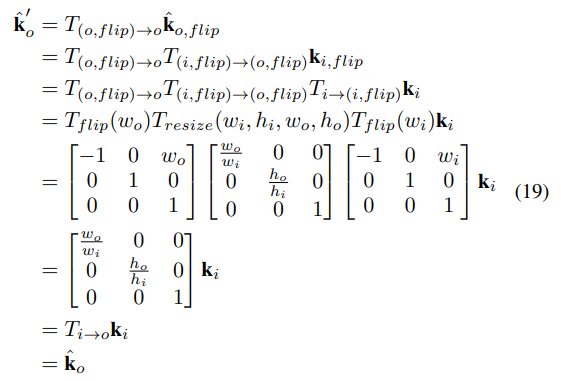
👉 결국 본 논문에서는 본인들이 만들어낸 이러한 Coordinate Transformation이 Bias를 일으키지 않는다는 것을 보여주었다.
3.1.6. Diagnosis of the Biased Coordinate System Transformation
이 챕터에서는 지금까지의 SOTA 모델들이 사용해온 Data Processing 문제에 대해 다룬다. 기존에 진행했던 Coordinate Transformation의 가장 큰 문제는 픽셀 해상도를 사용했다는 점이다. 이 때 Flipping Ensemble을 사용하면 아래와 같은 식이 만들어지게 되는데 이렇게 되면 원본 이미지의와 다른 예측 결과가 만들어지게 된다.

위 식에 따르면 $\frac{1-s}{s}$만큼의 x축 방향 Offset이 발생하며 이는 최종 예측에 상당한 오차를 유발한다.
이러한 문제를 해결하기 위해 Flipping된 이미지 결과를 평균 내기전에 1 Pixel을 보정하거나(SimpleBaseline, HRNet, DarkPose), HigherHRNet처럼 더 높은 출력 해상도를 사용하기도 하였으나 계산량의 증가나 예측 오류를 아예 없앨 수 없다는 단점이 있었다.
하지만 본 논문에서 제안하는 Unbiased Coordinate System Transform Pipeline은 이러한 문제를 근본적으로 해결하여 추가적인 보정 없이도 좋은 성능을 내게 만든다.
3.2. Unbiased Keypoint Format Transformation
논문 초반 부에 설명한 기존 Data Processing의 첫번째 문제점을 3.1.에서 해결하였으니 이번에는 두번째 문제점에 대해 다뤄보도록 하겠다.
3.2.1. The Concept of Unbiased Keypoint Format Transformation
지금까지는 관절 좌표를 Heatmap으로 변환하여 예측하는 것이 더 좋은 성능을 내는데 도움이 된다는 것이 정론이었다. 하지만 이 때 Keypoint에서 Heatmap으로(Encoding), Heatmap에서 Keypoint로(Decoding) 변환을 하는데 있어 Unbias를 유지하는 것이 중요하다. 만약 그렇지 않으면 Keypoint의 위치 정보가 왜곡되어 모델 성능이 저하 될 수 있다.
따라서 이번 챕터에서는 어떻게 하면 Keypoint-Heatmap 간의 상호 변환 과정을 Unbias하게 처리할 수 있을까? 에 대한 해결책을 제안한다.
3.2.2. Unbiased Keypoint Format Transformation
본 논문에서는 2 가지 Unbiased Keypoint Format Transformation 패러다임을 제안한다.
1. Combined Classification and Regression Format
이는 Object Detection에서 영감을 받아 설계된 것으로 분류 Heatmap과 회귀 Heatmap을 같이 사용한다.
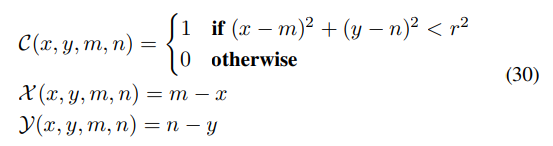
여기서 분류 Heatmap $C$는 Keypoint의 위치를 대략적으로 찾는 역할을 수행하며 $r$은 해당 영역을 Positive로 분류하는 범위를 의미하는 하이퍼 파라미터이다. 회귀 Heatmap $X$와 $Y$의 경우에는 분류 Heatmap이 제공하는 대략적인 위치에서의 Residual 정보를 보존한다(Offset Vector).
Loss로는 분류 Loss와 회귀 Loss를 모두 사용하며, Test 중에는 분류 Heatmap에서 가장 높은 Response $\hat{k}_h$를 찾고 예측된 Offset을 사용하여 정확한 Keypoint 위치를 업데이트 한다.
2. Classification Format
분류 Format에서는 이전 SOTA 모델들처럼 Gaussian 분포만을 사용한 Heatmap을 사용하여 Keypoint를 예측한다.
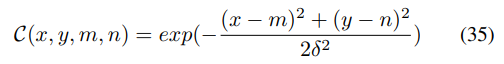
Loss로는 분류 Loss만을 정의하며, Test 중에는 DARK 방식을 통해 Decoding을 진행한다. 여기서 DARK. 방식이란 1차 도함수가 0이 되는 지점을 계산하는 방식으로 이렇게 Taylor 급수를 활용하면 Precision의 감소가 적어 Unbias 변환이 가능하다.
3.2.3. Analysis of Biased Keypoint Format Transformation
이번에는 기존에 사용하던 Biased Keypoint Format Transformation(SimpleBaseline, HRNet, HigherHRNet) 방법이 성능에 미치는 영향을 분석한다. 기존 방법과 본 논문에서 제안하는 방법과의 차이는 Encoding과정은 Gaussian 분포로 이루어진다는 점이 같지만, Decoding 과정에서 최적화되지 않은 방법을 사용한다는 것이다.
이 경우 1픽셀을 이동시키는 것으로 발생하는 기대 오차는 0.125 정도이며 높은 해상도로도 어느정도 문제를 해결할 수 있다.
👉 앞서 설명한 기존 모델들이 Bias 문제를 해결한 방법에 대한 증명
3.2.4. Join Analysis of Biased Coordinate System Transformation and Biased Keypoint Format Transformation
여기서는 지금까지 언급한 Biased Coordinate System Transformation과 Biased Keypoint Format Transformation이 같이 일어날 때 최종 결과에 미치는 영향에 대해 소개한다. 수식적인 분석 부분이 많아 짧게 요약한 내용은 다음과 같다.
- Coordinate System Transformation에 bias가 존재하여 변환시 좌표가 살짝 옆으로 변환된다.
- 살짝 옆으로 변환된 좌표를 가지고 Heatmap Encoding - Decoding을 진행한다.
- 이 때 Decoding 과정에서도 bias가 생기기 때문에 발생하는 기대오차는 0.375까지 커지게 된다.
결국 Bias가 발생하는 두가지 Transformation은 모두 최종적인 성능에 부정적인 영향을 미칠 수 있다.
4. Experiments
COCO 데이터 셋
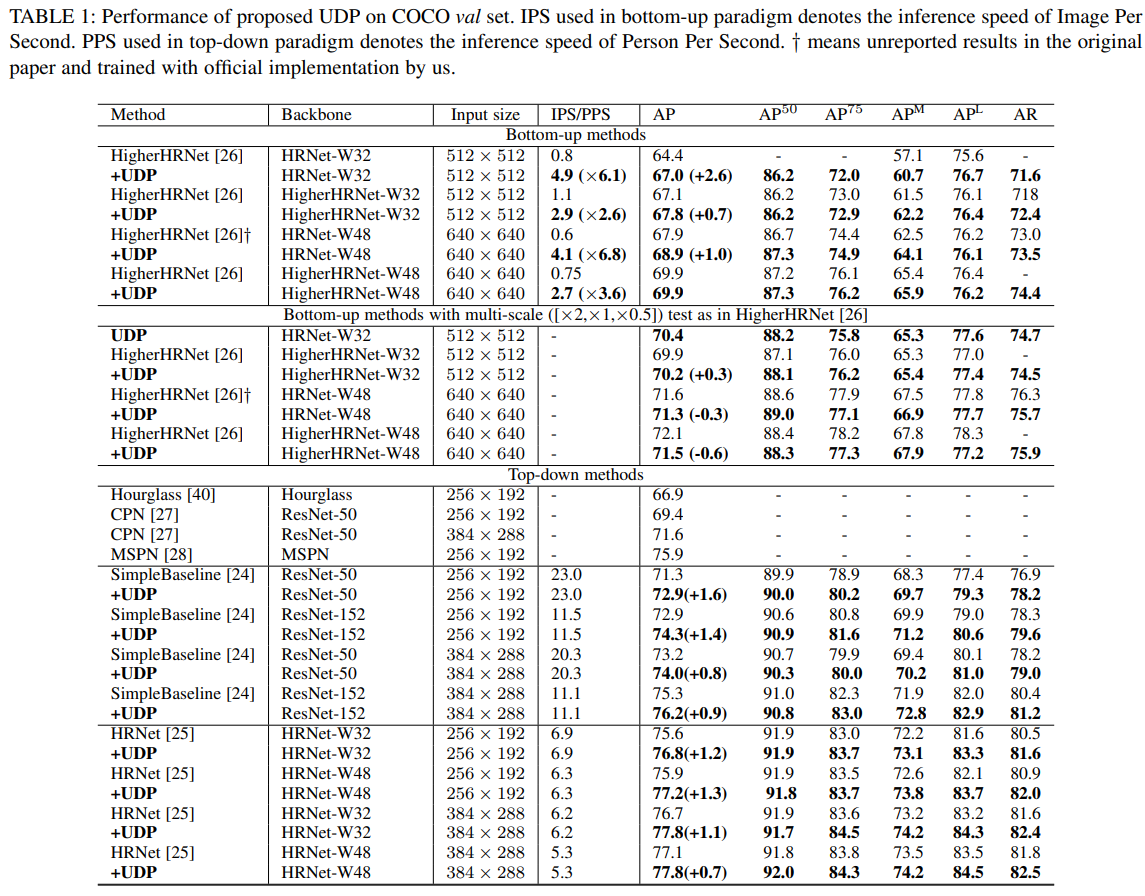
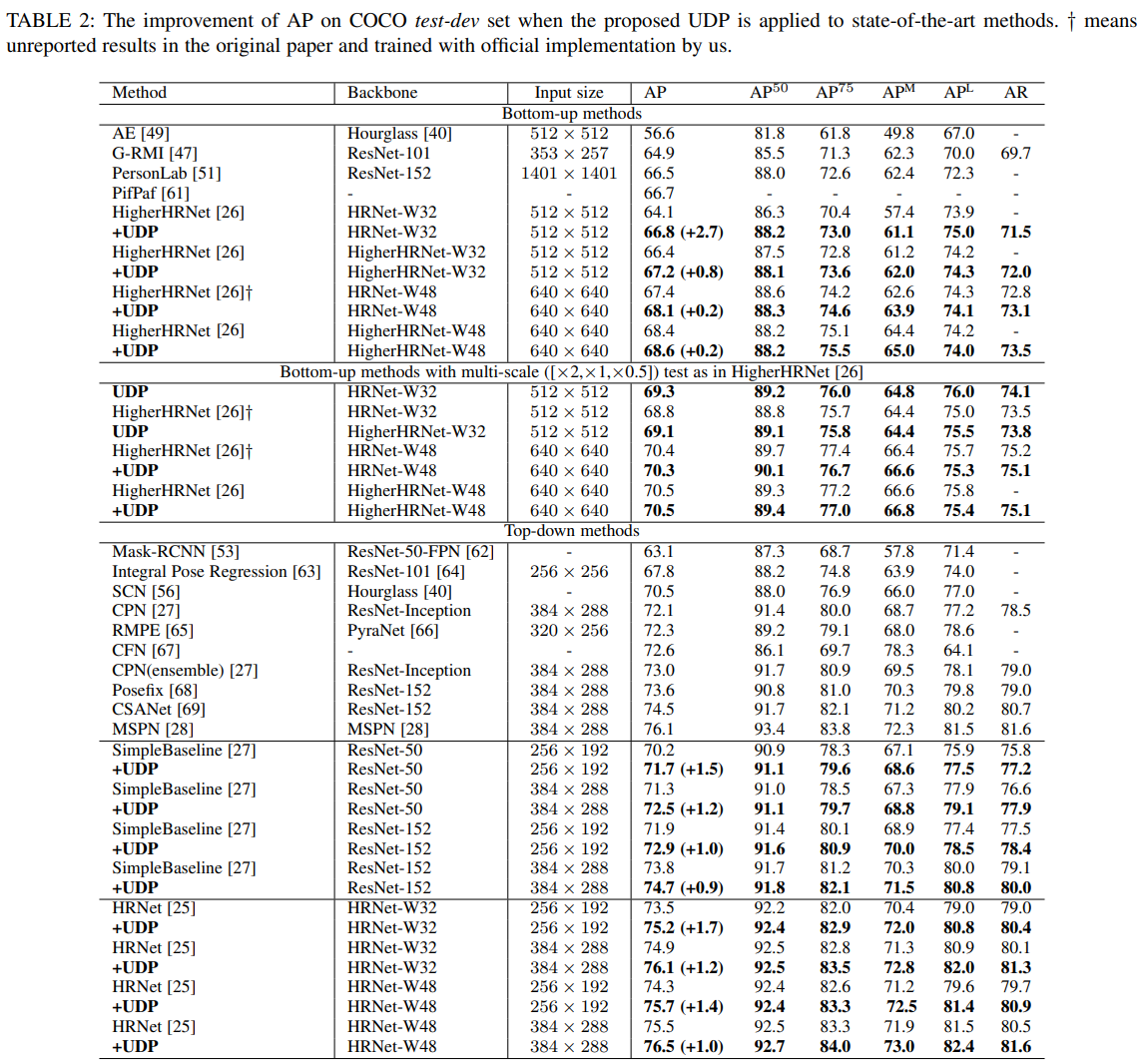
Bottom-Up 방식에서는 HigherHRNet, Top-Down 방식에서는 SimpleBaseline과 HRNet을 기준 모델로 사용하여 UDP 방법을 적용한 결과와 성능을 비교하였다. Unbiased Keypoint Format Transformation 방법으로는 Combined Classification and Regression Format 방식을 사용하였다.
두가지 방법에서 모두 성능이 향상되었으며 HigherHRNet에서는 추론 속도 또한 많이 빨라진 것을 확인할 수 있었다.
CrowdPose 데이터 셋
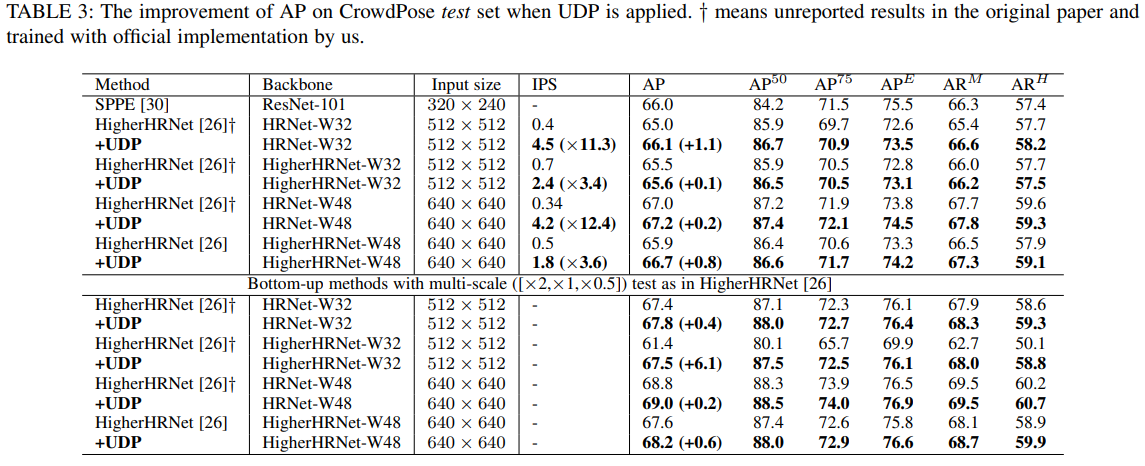
CrowdPose 데이터 셋에서도 좋은 성능을 보였다. 특히 HigherHRNet에서는 더 작은 해상도를 가진 HRNet을 Backbone으로 사용하고 UDP를 적용할 때 성능이 더 좋은 것을 볼 수 있는데 이를 통해 기존의 HigherHRNet의 네트워크 파이프라인이 너무 편향 되어있다고 주장한다.
Ablation Study
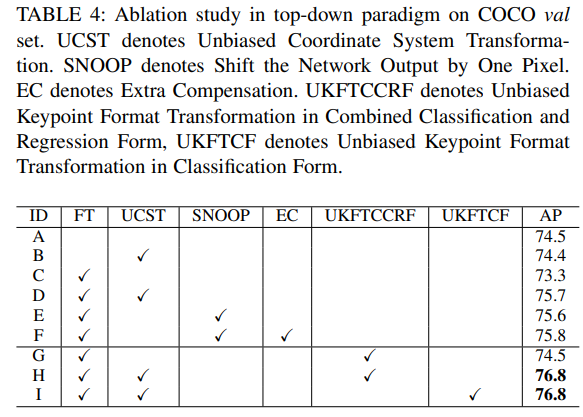
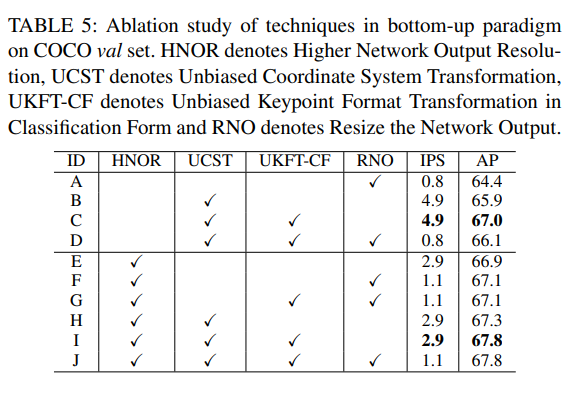
Top-Down 모델과 Bottom-Up 모델을 가지고 진행한 Ablation Study이다. 결국 Data Processing이 Pipeline 성능에 중요한 역할을 한다는 것을 보이고 있다.
이번 논문은 Human Pose Estimation Task에서의 데이터 전처리 방법에 대해 연구한 UDP 논문이다. 지금까지의 SOTA 모델들은 데이터 전처리에 대해 별다른 언급 없이 Flipping을 사용한다던가 Heatmap을 만든다는 언급만으로 넘어갔었는데 해당 방법이 진짜로 성능에 좋은 영향을 미치는지, 그렇지 않다면 어떤 방법이 더 좋은 성능을 만드는데 도움이 될 것 인지를 잘 보여주었던 논문이었다.
수학적인 증명 내용이 많아 읽기 까다로웠지만 그만큼 데이터 전처리의 중요성과 사소한 예측의 차이가 모델 성능에 많은 영향을 미친다는 것을 느낄 수 있었던 논문이었다. 코드를 통해 본문에서 크게 2가지로 나누어 제안한 UDP 방식이 어떻게 구현되어 있을지 확인하는 것이 필요할 것 같으며 추후 연구에서 어떻게 활용할 수 있을지, UDP 방식에서 나아가 더 발전된 데이터 전처리 방법이 있는지를 알아볼 필요가 있을 것 같다.
세 줄 요약
1. 기존 Human Pose Estimation 분야에서 사용한 Data Processing 방법에 문제를 지적하고 Unbias한 Data Processing 기법을 제안함
2. Bias가 생기는 원인을 Coordinate간의 Transformation과 Heatmap-Keypoint 간의 Transformation으로 지적하며 각각에 대응하여 Bias를 없앨 수 있는 방법을 제안함
3. Bias를 없애는 두 가지 방법이 결합된 UDP 기법을 기존 모델에 적용한 결과 Top-Down, Bottom-Up 모두에서 성능 개선이 일어난 것을 확인할 수 있었음
