[X:AI] DDPM 논문 이해하기

『 Denoising Diffusion Probabilistic Models. NeurIPS. 2020 』

최근 비전 태스크에서 매우 핫한 Diffusion Model들.. 그 기초가 되는 DDPM 논문을 톺아보도록 하자!!

 

들어가기 전에...

 

현재 이미지 생성 모델에는 여러 연구 방향이 존재하고 그 중 대표적으로는 GAN, VAE, Flow-based, Diffusion 방법이 존재한다. GAN과 VAE는 비슷한 시기에 등장하여 생성 모델에 많은 성능 향상을 이끌어 왔고 Diffusion은 최근 가장 핫한 방법론이라 불릴만큼 중요한 모델이다. 

 

이에 Diffusion에 대한 공부를 하기 전에 이 4가지 모델의 차이점이 어떻게 다른지 우선 알아보도록 하겠다.

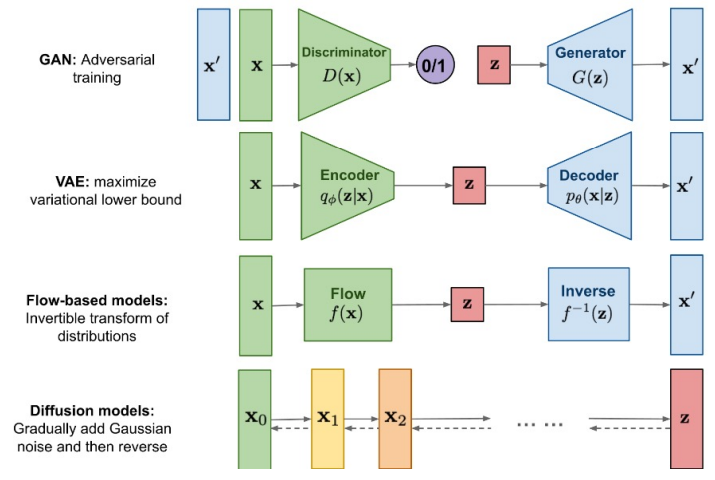
GAN(Generative Adversarial Network) : Generator와 Discriminator로 구분되어 가짜 데이터를 만드려는 Generator와 이를 구별하려는 Discriminator를 학습한다. 이 때 두 모델은 적대적인 경쟁을 통해 발전한다.

 

VAE(Variational AutoEncoder) : VAE는 확률적인 잠재 변수를 사용하여 데이터를 생성하는 모델이다. 데이터의 Latent Representation을 학습하는 것이 주요하며 이 때 확률 분포를 사용하여 데이터를 샘플링한다. 

 

Flow-based : 확률적인 데이터 분포를 변환하는 것이 주요하며 입력받은 데이터를 다른 확률 분포로 매핑한다. Implicit하게 학습되는 GAN이나 VAE와 달리 Latent Vector z를 역변환하여 Explicit하도록 입력 데이터의 분포를 학습한다. 

(VAE는 z의 확률분포를 Gaussian으로 근사하도록 만들지만, Flow-based는 x를 잘 표현하는 z를 만드는 f(x)를 학습하는게 주 목표이다!!)

어찌 보면 추천시스템의 Matrix Completion Task와 비슷하다는 느낌이 들었다...

 

Diffusion(확산) : 물질의 특정 분포가 와해되는 것을 의미하며 데이터로 생각한다면 특정 데이터의 패턴이 반복적인 과정을 거치며 와해되는 과정을 의미한다. 비지도 학습 방법론에서부터 시작되었고 그 중 이미지 생성 Task에서 현재 많이 활용되고 있다.

 

https://devkihyun.github.io/study/Flow-based-Generative-Models-1-Normalizing-Flow/

Flow based Generative Models 1 : Normalizing Flow

https://github.com/lucidrains/denoising-diffusion-pytorch

GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch

---

1. Introduction

DDPM을 말하기 전에 우선 DPM(Diffusion Probabilistic Models)을 알아보자. 

 

DPM(Diffusion Probabilistic Models)

• 현실의 Dataset을 확률 분포(Probability Distribution)으로 표현하는 것은 매우 어려우면서 중요한 문제이다. 이 때 Tractability와 Flexibility를 높이는 것이 중요한데, 이 둘은 Trade-Off 관계로 쉽게 이 문제를 해결하기는 어렵다. 
• Tractability : 데이터에 잘 적용되어 분석이 쉽고 계산이 용이한 분포인가
• Flexibility : 임의의 복잡한 데이터에 대해서도 잘 적용이 가능한가
• ex) 복잡한 데이터에 잘 적용되면서 계산이 쉬운 분포 == 찾기 어렵다!!

기존에 이러한 문제가 있어 DPM 모델은 아래의 과정으로 그 문제를 해결하고자 하였다.

 

• Data에 임의의 Noise를 더해주고(Forward Process) 해당 Noise를 제거하는 과정(Reverse Process)을 학습한다.
• Forward Process : Data에 Noise를 추가하며, Markov Chain 과정을 통해 Noise를 점차 추가해준다.
• Reverse Process : Gaussian Noise에서 시작하여 점차 Noise를 제거해 간다.

 

본 논문에서는 이러한 기존의 DPM 모델의 Loss와 Parameter 예측 방법을 더 학습이 잘 되도록 만들어주었다.

 

※ Markov Chain

: 이전 상태에서 다음 상태로 넘어갈 때 이전 상태만의 영향을 받는 확률 과정

https://angeloyeo.github.io/2020/09/17/MCMC.html

Markov Chain Monte Carlo - 공돌이의 수학정리노트 (Angelo's Math Notes)

 

2. Background

 

Forward Process

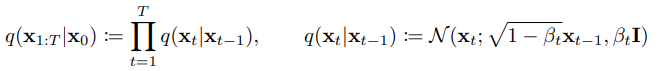
Markov Chain 과정을 거쳐 Data에 점차 Noise를 추가한다. 이 때 $x_t$와 $x_{t-1}$은 모든 과정에 있어 독립하며 Noise가 없는 $x_0$부터 시작해서 Gaussian Noise를 추가하고 마지막 $x_t$는 결국 Gaussian Noise 형태를 띈다. 

 

추가해지는 Gaussian Noise는 Gaussian 분포에서 Reparameterize , Sampling되며 오른쪽 수식과 같이 $\sqrt{1-B_t}$로 Scaling되는 이유는 분산이 발산하는 것을 방지하기 위해서이다. 하지만 이와같이 Step별로 t를 학습하게 될경우 많은 리소스가 들게 되고, 따라서 Closed Form으로의 수식 변환을 하면 다음과 같이 정리할 수 있다.

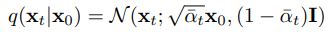
$$\alpha_t := 1 - \beta_t  \quad and \quad \bar{\alpha}:= \prod_{s=1}^{t}\alpha_s$$

 

Reverse Process

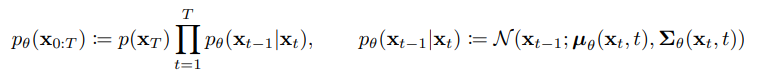
모델이 학습하는 Reverse Process로 Gaussian Noise를 없애가며 학습을 진행한다. VAE의 Decoding 과정과 비슷하며 실제로 알고 싶은 것은 $q(x_{t-1}|x_{t})$이지만 이걸 바로 알기 어렵기 때문에 이와 유사한 $p_{\theta}(x_{t-1}|x_t)$의 Parameter를 학습한다. 

 

 

Object Function

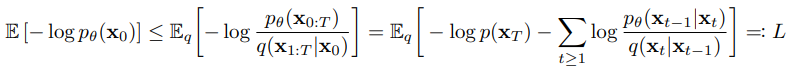
결국 Reverse Process 과정을 통해 $x_t$가 들어왔을 때 $x_{t-1}$를 학습하고 이는 결국 $x_0$까지 내려가게 된다. 이 때 생성된 이미지의 Negative Log Likelihood를 최소화하는 방식으로 위와 같이 Loss Function을 구성하고, 아래와 같이 정리된다.

Objective Function

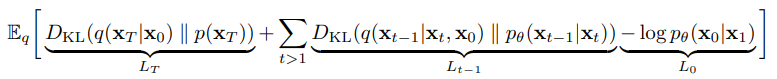
• 앞 단계는 Forward Process에서 DDPM이 항상 Gaussian Noise를 사용하기 때문에 $L_T$는 학습 과정에서 무시할만한 0에 가까운 상수이다.

 

3. Diffusion models and denoising autoencoders

3.1. Forward process and $L_T$

Forward Process는 위 Objective Function의 $L_T$에서 확인할 수 있다. 여기서는 $x_T$가 Gaussian 분포를 따르기 때문에 $q(x_T|x_0)$과 prior $p(x_T)$는 거의 유사한 값을 가진다. 또한 $B_t$를 일정하게 고정시킨후 Posterior를 정의하기 때문에 $q$에는 학습 파라미터가 없어 학습 과정에서 무시한다. 

 

3.2. Reverse process and $L_{1:T-1}$

다음 $L_{t-1}$은 Reverse(Denoising) Process의 목적식이다. 

 

이 때 모델의 output이 Gaussian Noise에 수렴하도록 하였다.

 

 

3.3. Data scaling, reverse process decoder, and $L_0$

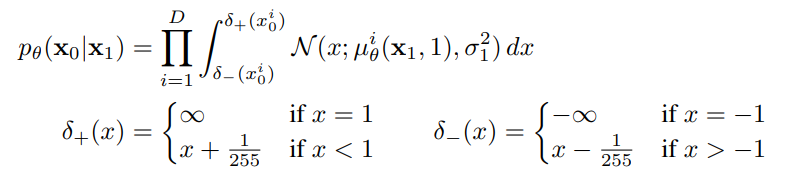
Reconstruction : $x_{t=0}$에 대해 $x_{t=1}$을 넣은 결과와 $x_{t=0}$과의 MSE Loss를 최소화

 

3.4. Simplified training objective

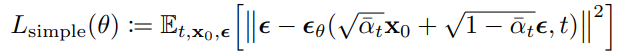
결국 DDPM 모델은 주어진 t 시점의 Gaussian Noise($\epsilon$)를 학습하며 다양한 Scale의 Gaussian Noise를 예측하여 Denoise에 활용하는 것이 목적이다. Coefficient Term을 제외한 Loss Term은 위와 같다. (뺀게 성능이 더 좋았음)

Loss의 Coefficient는 t가 커질때 작아지게 되기 때문에 Coefficient를 제거할 때 t가 큰 Process에 더 집중하게 된다. 즉, 이미지에 많은 Noise가 있을 때 Noise를 제거할 수 있게 된다. 

 

4. Experiments

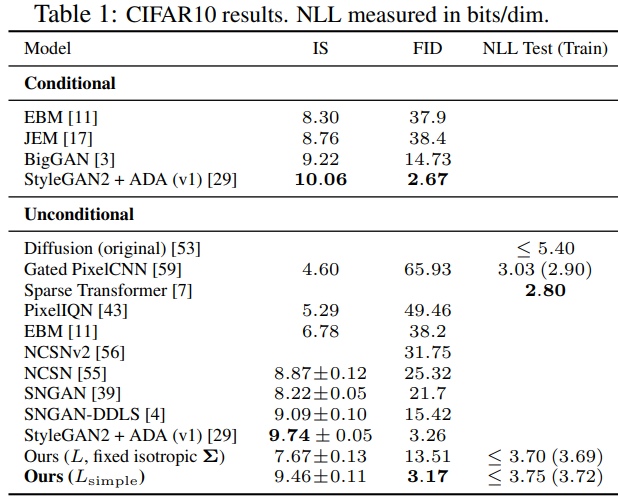
Sample Quality 수치

IS : Inception Score, 이미지의 품질과 다양성 측정

FID : Fréchet Inception Distance, 실제 이미지와 생성된 이미지에 대해 두 그룹이 얼마나 유사한지 벡터 사이의 거리를 측정

https://velog.io/@viriditass/GAN%EC%9D%80-%EC%95%8C%EA%B2%A0%EB%8A%94%EB%8D%B0-%EA%B7%B8%EB%9E%98%EC%84%9C-%EC%96%B4%EB%96%A4-GAN%EC%9D%B4-%EB%8D%94-%EC%A2%8B%EC%9D%80%EA%B1%B4%EB%8D%B0-How-to-evaluate-GAN

GAN은 알겠는데, 그래서 어떤 GAN이 더 좋은건데? Evaluating Generative Adversarial Networks

 

 

<참고 자료>

https://happy-jihye.github.io/diffusion/diffusion-1/

[Paper Review] DDPM: Denoising Diffusion Probabilistic Models 논문 리뷰

https://developers-shack.tistory.com/8

[논문공부] Denoising Diffusion Probabilistic Models (DDPM) 설명

https://developers-shack.tistory.com/9

[논문공부] Denoising Diffusion Probabilistic Models (DDPM) 설명 2

http://dsba.korea.ac.kr/seminar/?mod=document&uid=2352 

[Paper Review] Denoising Diffusion Probabilistic Model

---

세 줄 요약

1. 현재 다양한 Diffusion Model의 베이스가 되는 DDPM 모델 제안 
2. Forward Process로 Noise를 추가하고 Reverse Process로 Noise를 제거해하는 방식으로 모델을 설계
3. 수식 계산을 통해 목적 식을 제거하고 재구성 하여 특정 시점에서의 Gaussian Noise를 예측하는 Loss를 재정의, 안정적인 학습을 가능케 함