[Paper Review] Factorization Machines 논문 이해하기

『 Factorization Machines. 2010. 』

이번 논문은 추천 시스템 캡스톤 발표를 위해 읽은 Factorization Machines 논문이다. 이 논문에서는 기존에 사용하던 SVM, MF(Matrix Factorization)의 단점을 지적하며 SVM과 Factorization Model의 장점을 합친 FM(Factorization Machines) 모델을 제안한다. 

---

0. Abstract

추천 시스템은 주로 Sparsity가 큰 Rating Matrix 상에서 계산이 이루어진다. 하지만 기존 머신러닝에서 주로 사용되던 SVM(Support Vector Machine) 모델은 Sparsity 문제에서 잘 작동하지 않는다는 단점을 가진다. 따라서 이러한 문제를 극복하기 위해 본 논문에서는 FM(Factorization Machines)라는 새로운 모델을 제안한다.

 

SVM과 달리 FM은 Dual Form으로의 변환 없이도 모델 파라미터를 계산할 수 있고, 일반적인 입력 데이터에 대해서도 작동할 수 있어 FM에 대한 전문 지식이 없는 유저라도 쉽게 FM을 사용할 수 있다는 장점을 가진다. (SVD++, PITF, FPMC 와 같은 Factorization Model들은 특수한 입력 데이터에만 작동)

 

※ SVM(Support Vector Machine)

: 데이터를 분류하는 경계들 중 가장 큰 폭(margin)을 가진 경계를 찾는 알고리즘

 

https://ratsgo.github.io/machine%20learning/2017/05/23/SVM/

서포트 벡터 머신 (Support Vector Machine) · ratsgo's blog

 

1. Introduction

SVM은 머신러닝과 데이터 마이닝에서 가장 인기있는 예측 모델이지만, Sparse한 데이터가 제공되는 협업 필터링에서는 중요한 역할을 하지 못한다. 또한 Tensor/Specialized Factorization Model들은 표준 예측 데이터에 적용되지 않고, 특히 Specialize 한 모델은 모델링 및 설계가 필요한 특정 작업에 대해 개별적으로 파생된다.

 

FM(Factorization Machines)의 장점

(1) SVM이 실패하는 sparse한 데이터에서 parameter를 추정할 수 있다.

(2) Linear Complexity를 가지고 있다. 

(3) 어떠한 feature vector와 같이 작동할 수 있는 일반적인 Predictor이다.

 

2. Prediction Under Sparsity

일반적으로 예측 task에서는 실수 집합의 real valued feature vector x에서 target domain T를 만드는 함수 y를 찾는 분류 문제나 회귀 문제를 다루지만, 본 논문에서는 feature vector x가 sparse한 경우의 문제를 다룬다.

예를 들어 위의 예시처럼 User, Item, Data가 존재할 때 일반적인 Matrix Factorization 방식은 User, Item, Rating Matrix 만을 사용한다. 

Figure 1

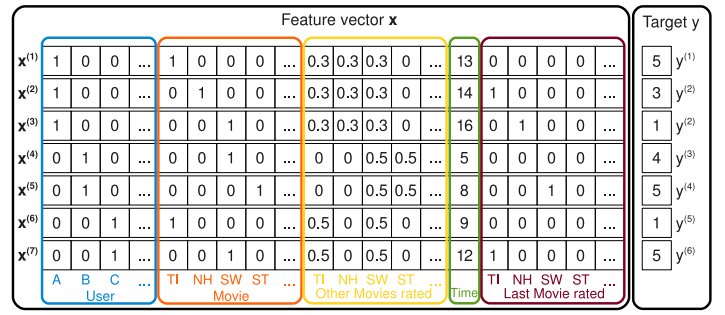
하지만 FM 방식은 가지고 있는 정보를 활용해 새로운 Feature를 만들고 합쳐 하나의 Feature Vector로 활용한다. 이 때 어떠한 Implicit 특성이든 Feature로 추가할 수 있고, 이 때 Feature는 원 핫 벡터 형태로 추가된다. (User, Item에 대한 정보를 n차원의 latent factor로 나타내는 Matrix Factorization 방법과 대조적)

 

첫 번째로 오는 부분(Blue)은 User에 대한 binary indicator 역할, 두 번째(Red)는 Movie에 대한 binary indicator이다. 그 뒤로 오는 Yellow 부분은 User가 평가한 다른 Item에 대한 정보로 그 합이 1이 되도록 정규화를 진행한다. 예를들어 4, 5행을 보면 같은 B 유저가 각각 SW, ST 영화에 대해 평가를 한 것을 확인할 수 있고, 이에 Yellow 파트에서 각각 0.5씩의 값을 준 것을 확인할 수 있다.

 

다음 Green 파트는 시간에 대한 정보(2009년 1월을 시작으로)를 담고 있고, Brown 파트는 마지막으로 평가한 영화에 대한 정보를 담고있다. (A User에 경우 TI - NH - SW 순으로 영화를 평가했으므로 2번째 행은 TI, 3번째 행은 NH에 대한 값이 Brown 파트에 저장)

 

위와 같이 한 Vector 안에 다양한 Feature가 포함되어 있기 때문에 SVM같은 일반적인 예측모델과 유사하고 Recommender System에 한정적이지 않아 어떠한 real valued feature vector에 적용할 수 있다.

 

3. Factorization Machines

3.A. Factorization Machine Model

(1) Model Equation

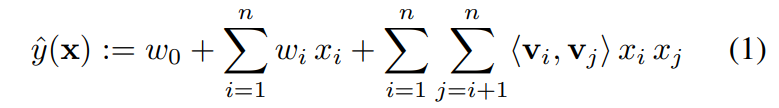
위 식은 dimension = 2로 2개의 Feature 사이의 관계를 고려한 FM 모델이다.

$$w_0 \in \mathbb{R},  w \in \mathbb{R}^n,  V \in \mathbb{R}^{n \times k}$$

$w_0$ : Global Bias

$w_i$ : i번째 변수 weight

$<v_i, v_j>$ : i번째 변수와 j번째 변수의 interaction (factorizing)

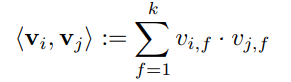
$k$ : Factorization 할 차원  

FM 모델은 Factorized Parametrization 방법을 사용하여 각각의 변수를 f 차원의 Latent Factor로 매핑하여 변수간의 상관관계를 나타낸다. 따라서 sparse 한 데이터의 경우에도 high-order interaction에 대한 파라미터 추정이 가능하다. 

 

(2) Expressiveness

$k$가 충분히 크다면 $W = V \cdot V^t$를 만족하는 matrix V는 존재한다. 즉, $k$가 충분히 클 경우 어떠한 크기의 interaction matrix $W$도 표현할 수 있다는 것이다. 

 

하지만 모든 복잡한 Interaction을 계산하기에는 데이터가 충분하지 않기 때문에 주로 작은 $k$를 선택한다. 이는 일반화 성능을 높이고 sparsity를 가진 상태에서 interaction matrix를 개선한다.

 

(3) Parameter Estimation Under Sparsity

데이터가 sparse해 변수들의 interaction을 측정하기 어렵더라도, FM 모델은 interaction parameter의 independence를 없애기 때문에 interaction을 측정할 수 있다. 

 

예시  
위의 Figure 1 그림에서 A유저의 ST영화에 대한 interaction을 측정하고 싶다고 해보자. 현재 데이터에는 A유저의 ST영화에 대한 정보가 없는 상태이다. 따라서 두 변수에 대한 직접적인 interaction을 계산할 경우 0이 된다. 하지만, Factorized Interaction parameter인 v를 사용한다면 이 경우에도 interaction을 계산할 수 있다. 

1. 유저 B와 C는 비슷한 factor vector를 가진다. 둘은 SW에 대해 비슷한 interaction(4, 5)을 가지기 때문에 두 벡터 모두 rating을 높이는 쪽으로 생겼을 것이기 때문 
2. 유저 A와 C는 다른 factor vector를 가진다. A가 Rating에서 TI와 SW에 대해 다른 interaction(TI에서는 5와 1, SW에서는 1과 5)을 가지기 때문
3. ST와 SW는 비슷한 factor vector를 가진다. 유저 B가 두 영화에 대해 비슷한 interaction(5, 4)을 가지기 때문

=> 결국 유저 A와 ST의 factor vector는 유저 A와 SW의 factor vector와 유사하다.
(또한, B와 비슷한 factor vector를 가진 C 또한 ST를 좋아할 것이라고 유추할 수 있다)

https://youtu.be/zYefA56NFcw?t=574 

 

(4) Computation

 

Model Equation이 만들어지기까지 아이디어가 뻗어나온 흐름을 살펴보자면, 우선 추천시스템에서 기본적으로 사용할 수 있는 모델은 아래 식과 같은 선형 모델이다.

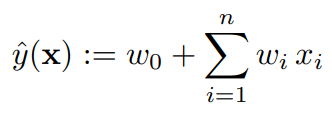
각각의 변수마다 가중치를 곱해주는 형태인데, 이 경우 계산이 단순하다는 장점이 있지만 변수간의 Interaction을 파악할 수 없다는 단점이 있다. 따라서 논문에서는 이러한 Interaction을 추가해 주기 위해 아래와 같은 가중치 수식을 추가해 준 것이다. (SVM의 Polynomial Kernel과 같이  모든 변수간의 상관관계를 모델링)

위 식에서 j가 i+1부터 시작하는 것은 같은 변수끼리의 Interaction은 고려하지 않고 a, b나 b, a나 같은 관계이기 때문에 한 쪽만 고려하겠다는 의미이다. 

 

하지만 이렇게 계산을 할 경우, Interaction을 고려한다는 점은 좋은데 시간 복잡도가 $O(kn^2)$이 된다는 단점이 생긴다. 따라서 논문에서는 아래와 같은 변환을 통해 $O(kn)$의 시간 복잡도를 가지도록 Equation을 변경하였다. 

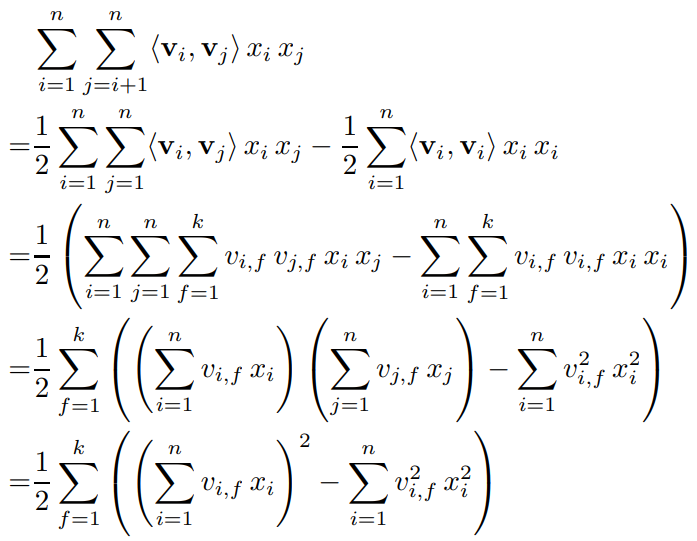
1->2 Line : 대칭행렬을 전체행렬에서 대각행렬을 빼고 1/2를 해준 것

2->3 Line : 위에 있는 $<v_i, v_j>$의 변환 값을 대입해준 것

3->4 Line : 안에 있는 sigma를 밖으로 빼주고 묶어줌

4->5 Line : 같은 값이므로 제곱으로 표현

 

https://youtu.be/7ubk_YXPRbA?t=248 

 

3.B. Factorization Machines as Predictors

FM 모델은 다양한 예측 task에 적용할 수 있다. 모든 경우에 Overfitting을 막기 위해 L2 정규화를 사용한다.

- 회귀(Regression)

- 분류(Binary Classification)

- 랭킹(Ranking)

 

3.C. Learning Factorization Machines

FM 모델은 선형적으로 계산되기 때문에 Gradient Method를 사용하면 모델 파라미터가 효율적으로 학습된다. (SGD와 같은 최적화, 다양한 loss function을 사용할 수 있음)

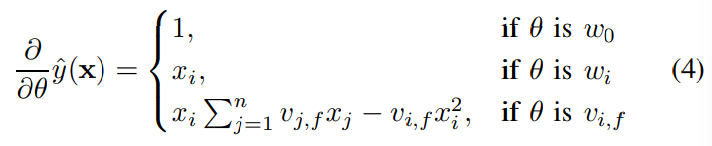
각각 $w_0, w_i, v_{i, f}$로 편미분한 gradient 값이다. 이 때 $\sum_{j=1}^n v_{j, f} x_j$는 $i$에 독립적이므로 먼저 계산할 수 있다.  

Gradient 계산 : $O(1)$  

Parameter 업데이트 : $O(kn)$ or $O(km(x))$  

 

3.D. d-way Factorization Machine

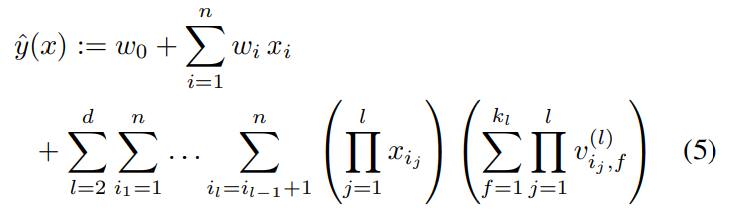
FM 모델은 일반화가 가능하고, d-way로 일반화한 수식 또한 Linear Complexity를 가진다. 

 

3.E. Summary

FM 모델은 factorized interaction으로 feature vector 사이에 가능한 모든 interaction을 모델링한다.

 

장점

(1) 높은 sparsity를 가지더라도 interaction을 계산할 수 있다. 따라서 관찰하지 못한 interaction의 일반화가 가능하다.

(2) 학습과 예측에 걸리는 시간뿐만 아니라 파라미터의 숫자도 linear하다. 따라서 SGD를 사용한 직접적인 최적화가 가능하고 다양한 손실함수를 사용해 최적화 할 수 있다. 

 

4. FMs vs SVMs

이 파트에서는 FM 모델과 SVM 모델의 차이점을 서술한다.

 

4.A. SVM Model

SVM의 Model Equation은 transformed input x와 model parameter w와의 dot product로 나타낼 수 있다. 

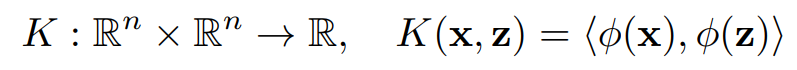
$\phi$ : feature vector인 $\mathbb{R}$를 더 complex한 $\mathcal{F}$ space로 매핑하는 함수로 Kernel과 위의 관계를 가진다.

 

(1) Linear Kernel

가장 간단한 형태의 커널로 $K_l(x,z) := 1+<x,z>$ 에서 $\phi(x) := (1, x_1, ..., x_n)$으로 매핑한다.

linear SVM은 아래의 식으로 나타난다. (d=1 일 때의 FM 식과 동일)

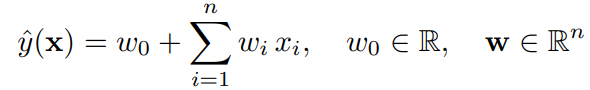
(2) Polynomial Kernel

Polynomial Kernel은 SVM 모델이 더 높은 차원의 Interaction을 가능케 한다. 

$K_l(x,z) := (1+<x,z>)^d$ 의 경우 $\phi(x)$는 아래와 같이 매핑한다. (d=2일 경우)

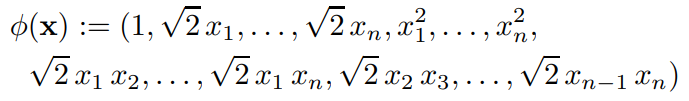
이 경우 식은 아래와 같이 나타난다.

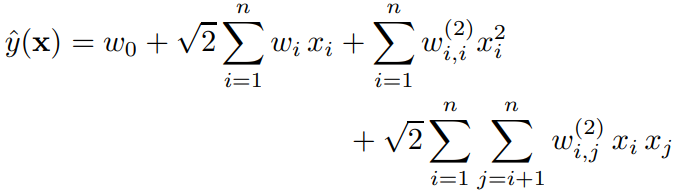
$w_{i, j}$의 Interaction이 반영된다는 점은 SVM과 FM이 동일하지만, FM이 공유하는 parameter를 가지는 것과 달리 SVM은 $w_{i, j}$가 모두 독립적이라는 차이점을 지닌다.

 

4.B. Parameter Estimation Under Sparsity

이 파트에서는 왜 linear, polynomial SVM이 sparse problem에서 실패하는지를 보여준다. Figure 1처럼 Sparse 한 데이터에서 오직 2가지 값만이 0이 아닌 상황을 가정하고 설명한다.

 

(1) Linear SVM

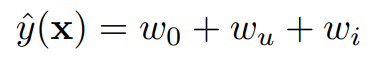
이 모델은 Collaborative Filtering에서 User나 Item 값이 파악되었을 때의 값과 같다. 모델이 단순하기 때문에 쉽게 파라미터를 예측할 수 있지만, 예측 수준은 낮다.  

Figure 2

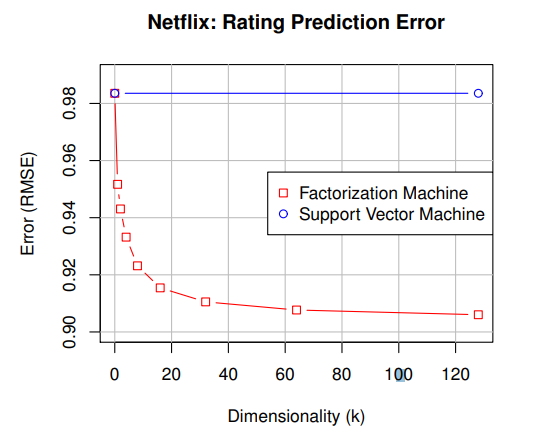
SVM 모델은 Sparse Data에서 학습이 잘 되지 않았고 FM 모델은 차원이 증가하며 Error가 줄어드는 것을 확인할 수 있다. 

 

(2) Polynomial SVM

Polynomial Kernel을 사용하면 고차원의 Interaction을 표현한다. m(x) = 2일 경우 Model Equation은 다음과 같다. 

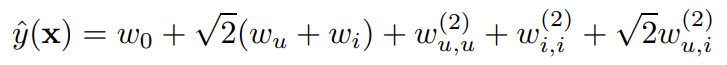
위 식에서 $w_u$와 $w^{(2)}_{u, u}$는 같은 것을 표현하기 때문에 하나는 제거할 수 있다. 그러면 기존 Linear Equation에  $w^{2}_{u, i}$가 추가된 형태인 것을 알 수 있다. 

 

여기서 $w^{2}_{u, i}$ 값은 학습 데이터에서 관측한 $(u, i)$이고 테스트 데이터에 $(u', i')$가 있다면 이 경우의 Interaction은 0이다. (Polynomial SVM은 User, Item에만 의존하기 때문에)

 

따라서 Polynomial SVM은 2-way Interaction 예측에 사용할 수 없고 Linear SVM보다 좋은 성능을 낼 수 없다. 

 

4.C. Summary

• SVM의 Parametrization에는 sparse setting에서 얻을 수 없는 Interaction에 대한 직접적인 관측치를 필요로 하기 때문에 FM과 달리 sparse 데이터에서 parameter를 추정하기 어렵다.
• FM 모델은 primal 하게 학습할 수 있지만, non-linear한 SVM 모델은 dual 하게 학습해야 한다.
• FM 모델의 Equation은 학습 데이터에 독립적이지만, SVM 모델의 예측은 학습 데이터에 종속적이다. 

https://pasus.tistory.com/91

[KKT 조건 - 3] 프라이멀 문제와 듀얼 문제

 

5. FMs vs Other Factorization Models

이 파트에서는 SVM을 제외한 다른 Factorization 모델 들을 어떤 식으로 모방하였고 그 차이에는 무엇이 있는지를 기술한다.

 

5.A. Matrix and Tensor Factorization

MF 모델은 가장 많이 연구된 Factorization 모델이다. User와 Item 2가지 categorical 변수들의 관계를 factorize하고 binary indicator로 정의하는 방식이다. 

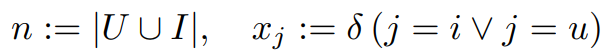
$x_j$가 $u$와 $i$에 대해 0이 아니기 때문에(User와 Item의 Interaction 존재), 이 feature vector를 사용하는 FM 모델은 MF 모델과 동일하다. 

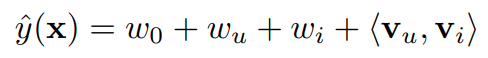
따라서 FM 모델의 식은 위와 같이 표현되어 $v_u, v_i$의 Interaction을 반영한다. 

 

5.B. SVD++

Regression과 같은 Rating Prediction Task에서 사용하는 SVD++ 모델을 모방하였다. 

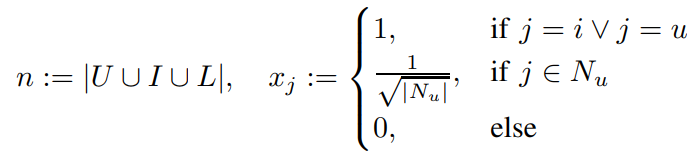
$N_u$ : 유저가 평가한 적이 있는 영화들의 집합  

FM 모델은 이 모델을 모방하여 위 feature vector x의 형태를 input으로 받는다.

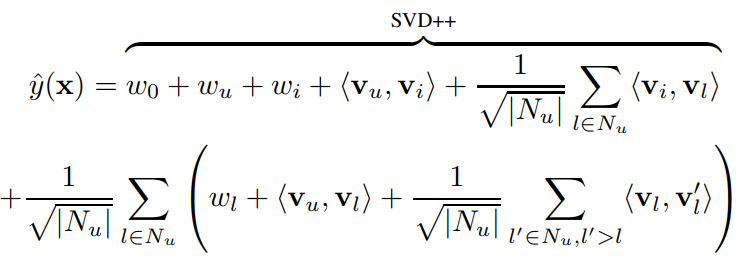
FM 모델은 초반은 SVD++ 모델과 동일하지만, 영화($N_u$)끼리의 Interaction이나 유저와 영화의 Interaction을 고려하는 부분을 포함한다.

 

5.C. PITF for Tag Recommendation

Tag Recommendation에서 좋은 성능을 보인 PITF 모델을 모방하였다. ($t$=tag)

FM 모델은 같은 User와 Item 조합안의 두 태그 사이에 랭킹이 사용되기 때문에 ($u, i, t_A$)와 ($u, i,t_B$) score 차이에 대한 최적화와 예측이 적용된다. 이를 고려하면 아래와 같은 식이 구성된다. 

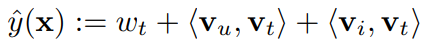
차이점

i) FM 모델은 t에 대한 bias term $w_t$를 가진다

ii) t에 대한 parameter $v_t$를 FM에서는 Interaction에서 공유하지만 PITF에서는 individual하다.

 

당시 SOTA 였던 PITF 모델과 비교해 보았을 때 파라미터 수에 따른 F1 score가 비슷하지만, Task에 대해 Specific 한 PITF 모델에 비해 General한 FM 모델이 우수함을 입증 

 

5.D. Factorized Personalized Markov Chains (FPMC)

FPMC 모델은 online shop에서 User의 마지막 구매를 기반으로 상품 순위를 정렬하는 모델이다. 

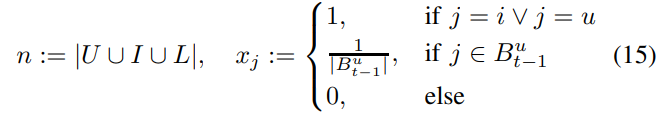
위와 같은 feature vector를 사용하고 여기서 $B^u_{t-1}$은 t 시점에서 User가 구매한 모든 Item을 말한다. 

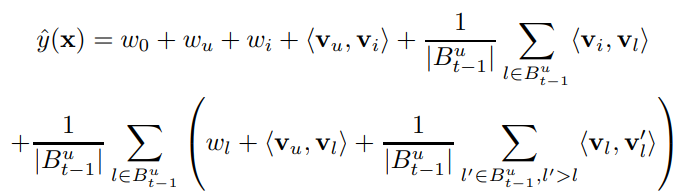
C의 Tag Recommendation 처럼 이 모델은 Ranking에 사용되기 때문에 ($u, i_A, t$)와 ($u, i_B, t$) 사이의 Score 차이가 prediction과 optimization의 기준으로 사용된다. 그러므로 위에서 추가된 식 중 $i$에 대한 식이 아닌 경우 사라지게 되어 아래의 FM 식이 만들어진다.

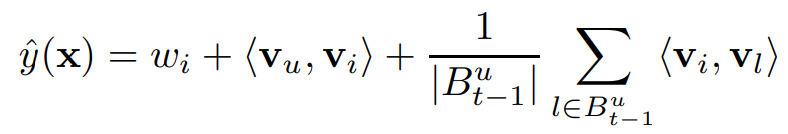
5.E. Summary

Specific task에 사용되는 위 모델들보다 Generalize하게 사용할 수 있는 FM 모델이 좋다.

 

6. Conclusion and Future Work

FM은 SVM과 Factorization model의 장점을 합친 모델이다.

(1) 큰 sparsity 아래서도 잘 작동하고

(2) 파라미터에 의존적이고 선형적인 equation을 가지며

(3) Primal에서 직접 최적화가 가능하다. 

FM 모델의 표현력은 Polynomial SVM과 비슷하며 Tensor Factorization 모델들과 대조적으로 어떠한 real valued vector를 다룰 수 있다. 또한 적절한 input feature vector를 사용하여 특정한 task에서 SOTA를 기록하고 있는 모델들과 동일하거나 비슷한 성능을 낼 수 있다. (MF, SVD++, PITF, FPMC 등)

 

 

<참고자료>

https://supkoon.tistory.com/31

[추천시스템][paper review][구현] Factorization Machines

https://velog.io/@jwj51720/%EB%85%BC%EB%AC%B8-Factorization-Machines

[논문 리뷰] Factorization Machines

https://greeksharifa.github.io/machine_learning/2019/12/21/FM/

Python, Machine & Deep Learning

---

세 줄 요약

1. SVM의 Generality + Factorization의 장점을 결합한 Factorization Machines 모델 제안
2. Sparse한 데이터에서도 쉽게 파라미터를 찾아낼 수 있고, 선형적인 복잡도를 가진다는 장점을 가짐
3. 추천 시스템 뿐만 아니라 다른 분야에서 사용되는 다양한 Factorization Model을 모방할 수 있다.